
Question Number 183246 by cortano1 last updated on 24/Dec/22
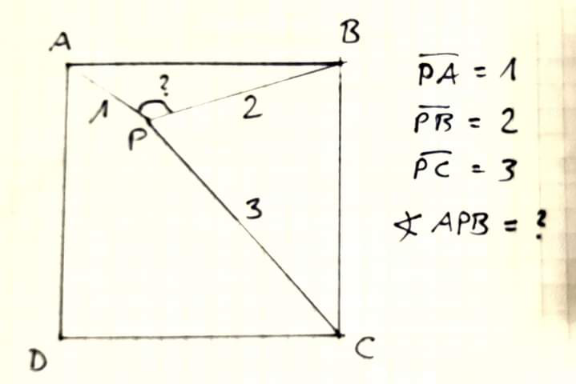
Answered by mr W last updated on 24/Dec/22
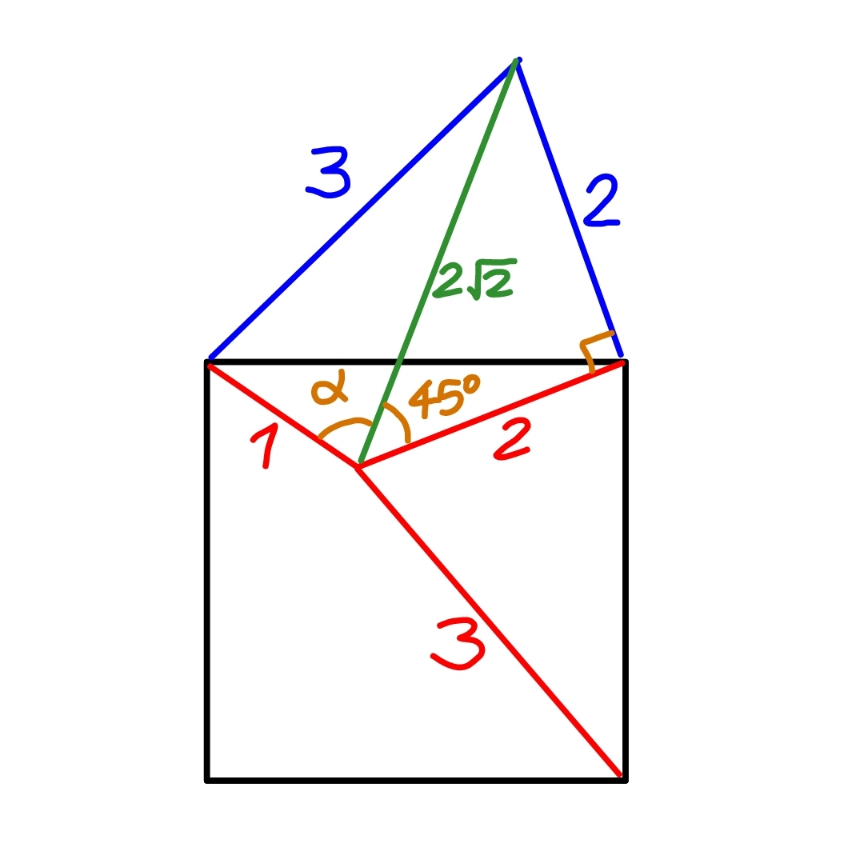
Commented by mr W last updated on 24/Dec/22
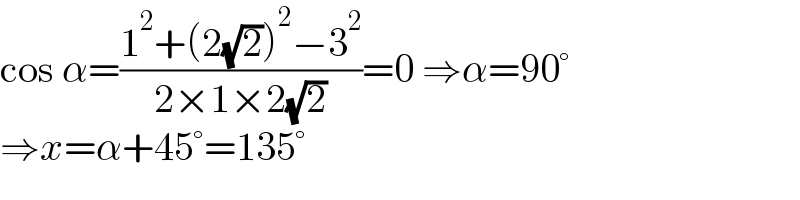
$$\mathrm{cos}\:\alpha=\frac{\mathrm{1}^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }{\mathrm{2}×\mathrm{1}×\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{0}\:\Rightarrow\alpha=\mathrm{90}° \\ $$$$\Rightarrow{x}=\alpha+\mathrm{45}°=\mathrm{135}° \\ $$
Commented by cortano1 last updated on 24/Dec/22

$${nice} \\ $$
Answered by HeferH last updated on 24/Dec/22
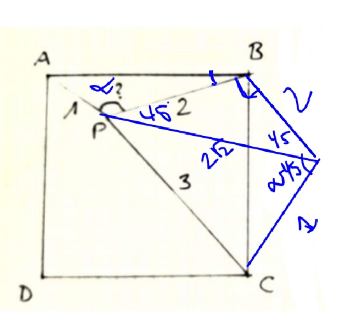
Commented by HeferH last updated on 24/Dec/22

$$\:\mathrm{3}^{\mathrm{2}} \:=\:\mathrm{1}^{\mathrm{2}} \:+\:\left(\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:\Rightarrow\:{right}\:{triangle}\: \\ $$$$\alpha\:−\:\mathrm{45}°\:=\:\mathrm{90}° \\ $$$$\:\alpha\:=\:\mathrm{135}° \\ $$
Commented by cortano1 last updated on 24/Dec/22

$${great} \\ $$
Answered by SEKRET last updated on 04/Jan/23
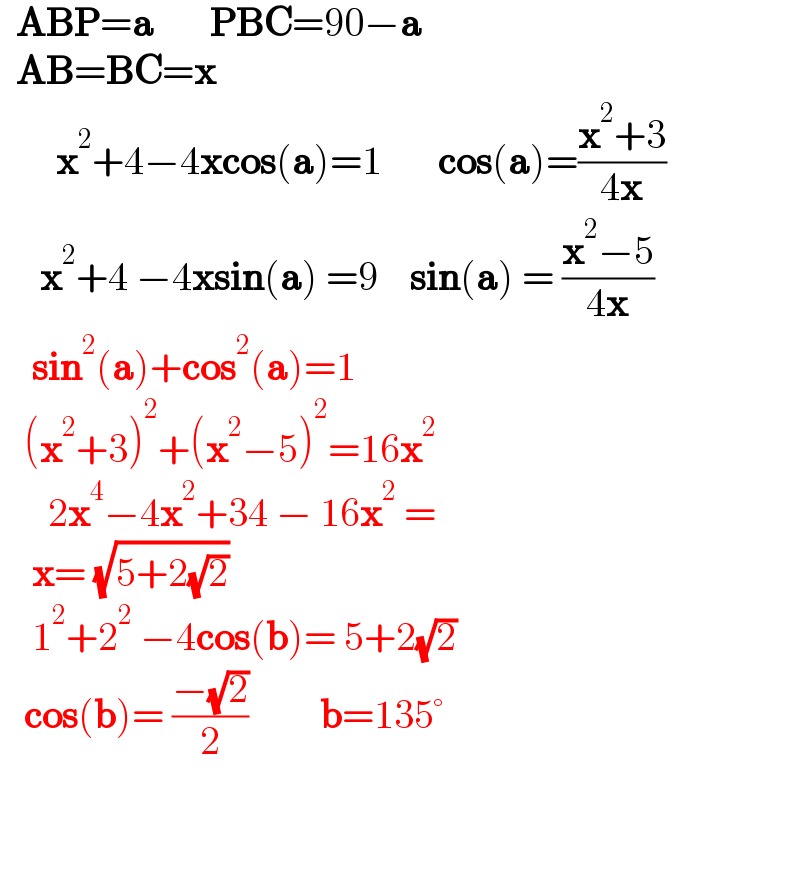
$$\:\:\boldsymbol{\mathrm{ABP}}=\boldsymbol{\mathrm{a}}\:\:\:\:\:\:\:\boldsymbol{\mathrm{PBC}}=\mathrm{90}−\boldsymbol{\mathrm{a}} \\ $$$$\:\:\boldsymbol{\mathrm{AB}}=\boldsymbol{\mathrm{BC}}=\boldsymbol{\mathrm{x}} \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{4}−\mathrm{4}\boldsymbol{\mathrm{xcos}}\left(\boldsymbol{\mathrm{a}}\right)=\mathrm{1}\:\:\:\:\:\:\:\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{a}}\right)=\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{3}}{\mathrm{4}\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{4}\:−\mathrm{4}\boldsymbol{\mathrm{xsin}}\left(\boldsymbol{\mathrm{a}}\right)\:=\mathrm{9}\:\:\:\:\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{a}}\right)\:=\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}}{\mathrm{4}\boldsymbol{\mathrm{x}}} \\ $$$$\:\:\:\:\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{a}}\right)+\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{a}}\right)=\mathrm{1} \\ $$$$\:\:\:\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\mathrm{5}\right)^{\mathrm{2}} =\mathrm{16}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{2}\boldsymbol{\mathrm{x}}^{\mathrm{4}} −\mathrm{4}\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\mathrm{34}\:−\:\mathrm{16}\boldsymbol{\mathrm{x}}^{\mathrm{2}} \:= \\ $$$$\:\:\:\:\boldsymbol{\mathrm{x}}=\:\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\:\:\:\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} \:−\mathrm{4}\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{b}}\right)=\:\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:\:\:\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{b}}\right)=\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}=\mathrm{135}° \\ $$$$ \\ $$$$ \\ $$
