Question and Answers Forum

All Questions      Topic List

Vector Questions

Previous in All Question      Next in All Question      

Previous in Vector      Next in Vector      

Question Number 183165 by universe last updated on 21/Dec/22

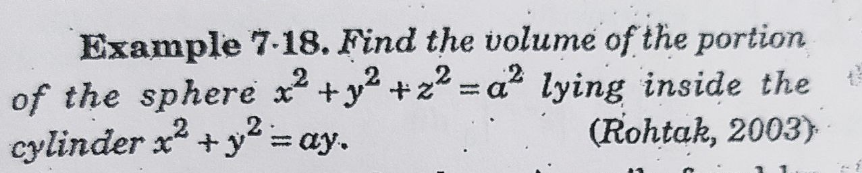
Answered by mr W last updated on 22/Dec/22

Commented by mr W last updated on 21/Dec/22

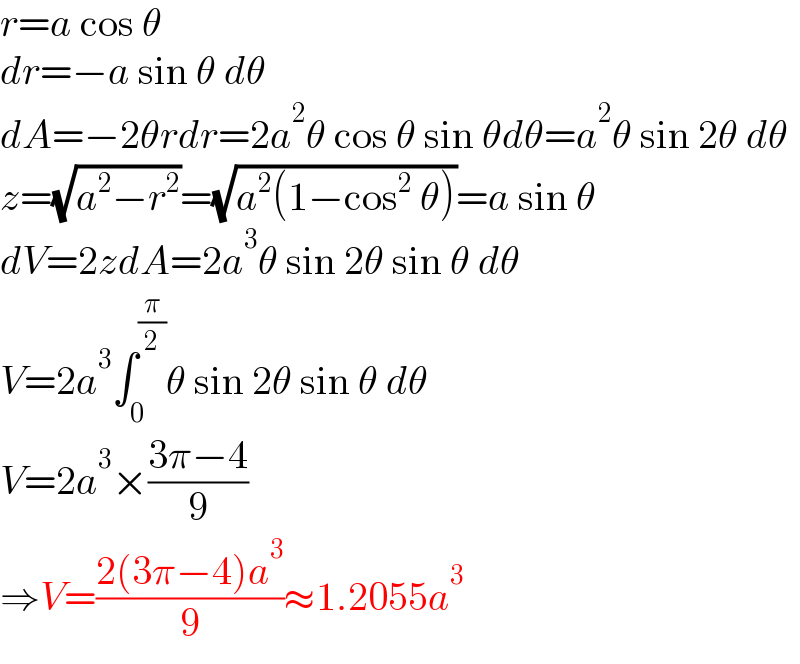
r=a cos θ dr=−a sin θ dθ dA=−2θrdr=2a^2 θ cos θ sin θdθ=a^2 θ sin 2θ dθ z=(√(a^2 −r^2 ))=(√(a^2 (1−cos^2 θ)))=a sin θ dV=2zdA=2a^3 θ sin 2θ sin θ dθ V=2a^3 ∫_0 ^(π/2) θ sin 2θ sin θ dθ V=2a^3 ×((3π−4)/9) ⇒V=((2(3π−4)a^3 )/9)≈1.2055a^3

$${r}={a}\:\mathrm{cos}\:\theta \\ $$$${dr}=−{a}\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${dA}=−\mathrm{2}\theta{rdr}=\mathrm{2}{a}^{\mathrm{2}} \theta\:\mathrm{cos}\:\theta\:\mathrm{sin}\:\theta{d}\theta={a}^{\mathrm{2}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:{d}\theta \\ $$$${z}=\sqrt{{a}^{\mathrm{2}} −{r}^{\mathrm{2}} }=\sqrt{{a}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta\right)}={a}\:\mathrm{sin}\:\theta \\ $$$${dV}=\mathrm{2}{zdA}=\mathrm{2}{a}^{\mathrm{3}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${V}=\mathrm{2}{a}^{\mathrm{3}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{sin}\:\theta\:{d}\theta \\ $$$${V}=\mathrm{2}{a}^{\mathrm{3}} ×\frac{\mathrm{3}\pi−\mathrm{4}}{\mathrm{9}} \\ $$$$\Rightarrow{V}=\frac{\mathrm{2}\left(\mathrm{3}\pi−\mathrm{4}\right){a}^{\mathrm{3}} }{\mathrm{9}}\approx\mathrm{1}.\mathrm{2055}{a}^{\mathrm{3}} \\ $$

Commented by universe last updated on 22/Dec/22

thanks sir

$${thanks}\:{sir} \\ $$

Commented by mr W last updated on 22/Dec/22

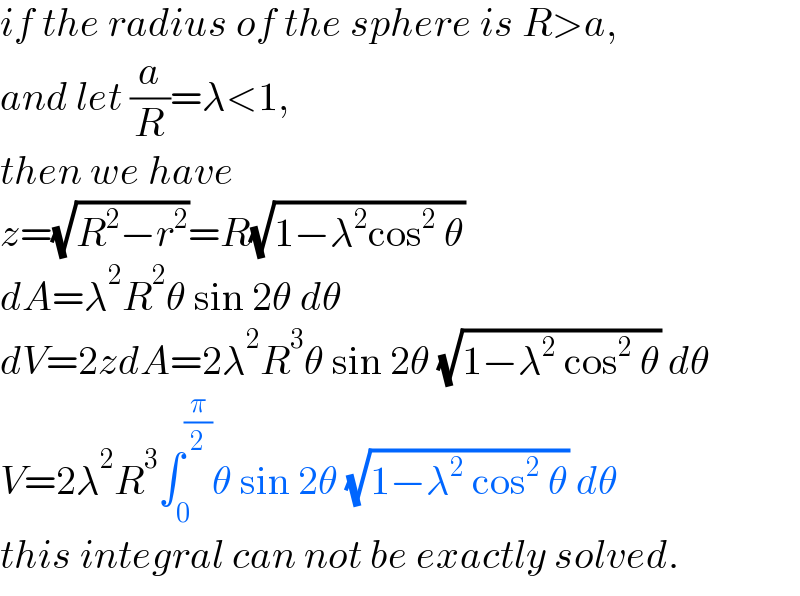
if the radius of the sphere is R>a, and let (a/R)=λ<1, then we have z=(√(R^2 −r^2 ))=R(√(1−λ^2 cos^2 θ)) dA=λ^2 R^2 θ sin 2θ dθ dV=2zdA=2λ^2 R^3 θ sin 2θ (√(1−λ^2 cos^2 θ)) dθ V=2λ^2 R^3 ∫_0 ^(π/2) θ sin 2θ (√(1−λ^2 cos^2 θ)) dθ this integral can not be exactly solved.

$${if}\:{the}\:{radius}\:{of}\:{the}\:{sphere}\:{is}\:{R}>{a}, \\ $$$${and}\:{let}\:\frac{{a}}{{R}}=\lambda<\mathrm{1}, \\ $$$${then}\:{we}\:{have} \\ $$$${z}=\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }={R}\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$${dA}=\lambda^{\mathrm{2}} {R}^{\mathrm{2}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:{d}\theta \\ $$$${dV}=\mathrm{2}{zdA}=\mathrm{2}\lambda^{\mathrm{2}} {R}^{\mathrm{3}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\:{d}\theta \\ $$$${V}=\mathrm{2}\lambda^{\mathrm{2}} {R}^{\mathrm{3}} \int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \theta\:\mathrm{sin}\:\mathrm{2}\theta\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\theta}\:{d}\theta \\ $$$${this}\:{integral}\:{can}\:{not}\:{be}\:{exactly}\:{solved}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com