
Question Number 183162 by mnjuly1970 last updated on 21/Dec/22

Answered by aleks041103 last updated on 23/Dec/22
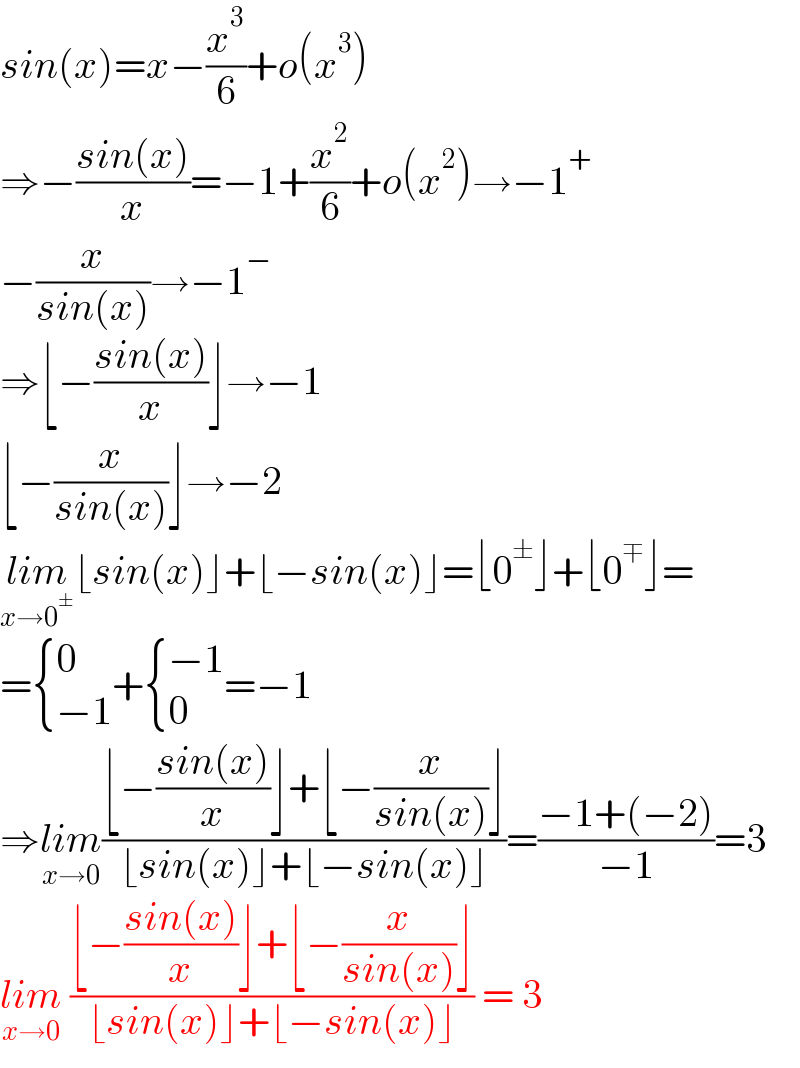
$${sin}\left({x}\right)={x}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{3}} \right) \\ $$$$\Rightarrow−\frac{{sin}\left({x}\right)}{{x}}=−\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{6}}+{o}\left({x}^{\mathrm{2}} \right)\rightarrow−\mathrm{1}^{+} \\ $$$$−\frac{{x}}{{sin}\left({x}\right)}\rightarrow−\mathrm{1}^{−} \\ $$$$\Rightarrow\lfloor−\frac{{sin}\left({x}\right)}{{x}}\rfloor\rightarrow−\mathrm{1} \\ $$$$\lfloor−\frac{{x}}{{sin}\left({x}\right)}\rfloor\rightarrow−\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{\pm} } {{lim}}\lfloor{sin}\left({x}\right)\rfloor+\lfloor−{sin}\left({x}\right)\rfloor=\lfloor\mathrm{0}^{\pm} \rfloor+\lfloor\mathrm{0}^{\mp} \rfloor= \\ $$$$=\begin{cases}{\mathrm{0}}\\{−\mathrm{1}}\end{cases}+\begin{cases}{−\mathrm{1}}\\{\mathrm{0}}\end{cases}=−\mathrm{1} \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{\lfloor−\frac{{sin}\left({x}\right)}{{x}}\rfloor+\lfloor−\frac{{x}}{{sin}\left({x}\right)}\rfloor}{\lfloor{sin}\left({x}\right)\rfloor+\lfloor−{sin}\left({x}\right)\rfloor}=\frac{−\mathrm{1}+\left(−\mathrm{2}\right)}{−\mathrm{1}}=\mathrm{3} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\lfloor−\frac{{sin}\left({x}\right)}{{x}}\rfloor+\lfloor−\frac{{x}}{{sin}\left({x}\right)}\rfloor}{\lfloor{sin}\left({x}\right)\rfloor+\lfloor−{sin}\left({x}\right)\rfloor}\:=\:\mathrm{3} \\ $$
Commented by mnjuly1970 last updated on 29/Dec/22

$${bravo}\:{sir} \\ $$
