
Question Number 182571 by Khalmohmmad last updated on 11/Dec/22
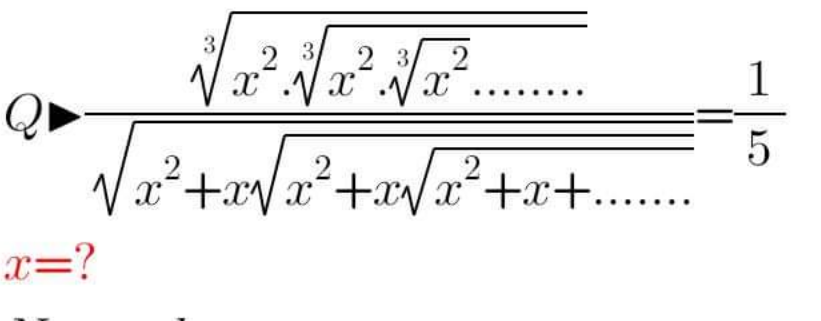
Answered by aleks041103 last updated on 11/Dec/22

$$\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} .\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} .\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} ....}}}={y}\Rightarrow{y}=\sqrt[{\mathrm{3}}]{{x}^{\mathrm{2}} {y}} \\ $$$$\Rightarrow{y}^{\mathrm{3}} ={x}^{\mathrm{2}} {y}\Rightarrow{y}=\pm{x},\:{but}\:{obv}.\:{y}>\mathrm{0}\Rightarrow{y}=\mid{x}\mid \\ $$$$\sqrt{{x}^{\mathrm{2}} +{x}\sqrt{{x}^{\mathrm{2}} +{x}\sqrt{{x}^{\mathrm{2}} +{x}....}}}={z} \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} +{xz}}={z} \\ $$$$\Rightarrow{z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{xz}\Rightarrow{z}^{\mathrm{2}} −{xz}−{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{z}_{\mathrm{1}/\mathrm{2}} =\frac{{x}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}}{x} \\ $$$${but}\:{z}>\mathrm{0}\Rightarrow{z}=\begin{cases}{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}{x},\:{x}>\mathrm{0}}\\{\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}{x},\:{x}<\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\mathrm{5}=\begin{cases}{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\frac{{x}}{\mid{x}\mid},{x}>\mathrm{0}}\\{\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\frac{{x}}{\mid{x}\mid},{x}<\mathrm{0}}\end{cases}=\begin{cases}{\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},{x}>\mathrm{0}}\\{{undef}\:{x}=\mathrm{0}}\\{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}},{x}<\mathrm{0}}\end{cases} \\ $$$$\Rightarrow{No}\:{solution}! \\ $$
