
Question Number 182512 by mathlove last updated on 10/Dec/22
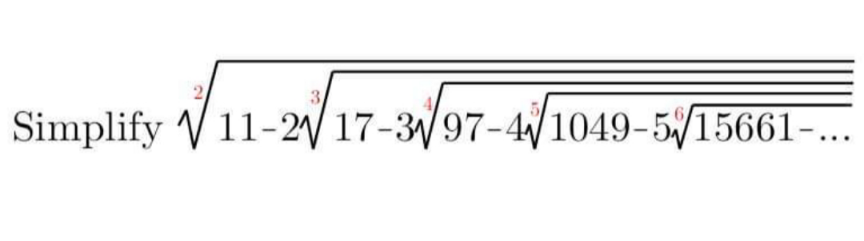
Answered by manxsol last updated on 10/Dec/22

$$\sqrt{\mathrm{7}} \\ $$
Answered by manxsol last updated on 11/Dec/22
![analisis 11−2a_1 ⟩0⇒a_1 ⟨5.5 0⟨ x ⟨(√(11)) x=(√(11−2a_1 )) a_1 =^3 (√(17−3a_2 )) a_2 =^4 (√(97−4a_3 )) a_3 =^5 (√(1049−5d)) ....=...... x^2 =11−2a_1 a_1 ^3 =17−3a_2 a_2 ^4 =97−4a_3 a_3 ^5 =1048−5a_4 .......................... x^2 −7=2^2 −2a_1 a_1 ^3 =2^3 +3^2 −3a_2 a_2 ^4 =3^4 +4^2 −4a_3 a_3 ^5 =4^5 +5^2 −5a_4 ............................. x^2 −7=2(2−a_1 ) a_1 ^3 −2^3 =3(3−a_2 ) a_2 ^4 −3^4 =4(4−a_3 ) a_3 ^5 −4^5 =5(5−a_4 ) .......................... x^2 −7=2(2−a_1 ) (a_1 −2)P_1 =3(3−a_2 ) (a_2 −3)P_2 =4(4−a_3 ) (a_3 −4)P_3 =5(5−a_4 ) P_n =[a_n ^(n+2) −(n+1)^(n+2) ]/[a_n −(n+1)] ..................... multiplication (x^2 −7)P_1 P_2 P_3 ...=2.3.4.5 x^2 −7=((n!)/(P_1 P_2 P_(3......) )) x^2 =7+((n!)/(∐Pn)) n⇒∞⇒((n!)/(∐P_n ))⇒0 ∴x^2 =7 x=(√7) x=(√7) approves initial condition](Q182541.png)
$${analisis}\:\:\:\:\mathrm{11}−\mathrm{2}{a}_{\mathrm{1}} \rangle\mathrm{0}\Rightarrow{a}_{\mathrm{1}} \langle\mathrm{5}.\mathrm{5} \\ $$$$\mathrm{0}\langle\:{x}\:\langle\sqrt{\mathrm{11}} \\ $$$$ \\ $$$${x}=\sqrt{\mathrm{11}−\mathrm{2}{a}_{\mathrm{1}} } \\ $$$${a}_{\mathrm{1}} =^{\mathrm{3}} \sqrt{\mathrm{17}−\mathrm{3}{a}_{\mathrm{2}} } \\ $$$${a}_{\mathrm{2}} =^{\mathrm{4}} \sqrt{\mathrm{97}−\mathrm{4}{a}_{\mathrm{3}} } \\ $$$${a}_{\mathrm{3}} =^{\mathrm{5}} \sqrt{\mathrm{1049}−\mathrm{5}{d}} \\ $$$$....=...... \\ $$$${x}^{\mathrm{2}} =\mathrm{11}−\mathrm{2}{a}_{\mathrm{1}} \\ $$$${a}_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{17}−\mathrm{3}{a}_{\mathrm{2}} \\ $$$${a}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{97}−\mathrm{4}{a}_{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} ^{\mathrm{5}} =\mathrm{1048}−\mathrm{5}{a}_{\mathrm{4}} \\ $$$$.......................... \\ $$$${x}^{\mathrm{2}} −\mathrm{7}=\mathrm{2}^{\mathrm{2}} −\mathrm{2}{a}_{\mathrm{1}} \\ $$$${a}_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{2}^{\mathrm{3}} +\mathrm{3}^{\mathrm{2}} −\mathrm{3}{a}_{\mathrm{2}} \\ $$$${a}_{\mathrm{2}} ^{\mathrm{4}} =\mathrm{3}^{\mathrm{4}} +\mathrm{4}^{\mathrm{2}} −\mathrm{4}{a}_{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} ^{\mathrm{5}} =\mathrm{4}^{\mathrm{5}} +\mathrm{5}^{\mathrm{2}} −\mathrm{5}{a}_{\mathrm{4}} \\ $$$$............................. \\ $$$${x}^{\mathrm{2}} −\mathrm{7}=\mathrm{2}\left(\mathrm{2}−{a}_{\mathrm{1}} \right) \\ $$$${a}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{2}^{\mathrm{3}} =\mathrm{3}\left(\mathrm{3}−{a}_{\mathrm{2}} \right) \\ $$$${a}_{\mathrm{2}} ^{\mathrm{4}} −\mathrm{3}^{\mathrm{4}} =\mathrm{4}\left(\mathrm{4}−{a}_{\mathrm{3}} \right) \\ $$$${a}_{\mathrm{3}} ^{\mathrm{5}} −\mathrm{4}^{\mathrm{5}} =\mathrm{5}\left(\mathrm{5}−{a}_{\mathrm{4}} \right) \\ $$$$.......................... \\ $$$${x}^{\mathrm{2}} −\mathrm{7}=\mathrm{2}\left(\mathrm{2}−{a}_{\mathrm{1}} \right) \\ $$$$\left({a}_{\mathrm{1}} −\mathrm{2}\right){P}_{\mathrm{1}} =\mathrm{3}\left(\mathrm{3}−{a}_{\mathrm{2}} \right) \\ $$$$\left({a}_{\mathrm{2}} −\mathrm{3}\right){P}_{\mathrm{2}} =\mathrm{4}\left(\mathrm{4}−{a}_{\mathrm{3}} \right) \\ $$$$\left({a}_{\mathrm{3}} −\mathrm{4}\right){P}_{\mathrm{3}} =\mathrm{5}\left(\mathrm{5}−{a}_{\mathrm{4}} \right) \\ $$$${P}_{{n}} =\left[{a}_{{n}} ^{{n}+\mathrm{2}} −\left({n}+\mathrm{1}\right)^{{n}+\mathrm{2}} \right]/\left[{a}_{{n}} −\left({n}+\mathrm{1}\right)\right] \\ $$$$..................... \\ $$$${multiplication} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{7}\right){P}_{\mathrm{1}} {P}_{\mathrm{2}} {P}_{\mathrm{3}} ...=\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{5} \\ $$$${x}^{\mathrm{2}} −\mathrm{7}=\frac{{n}!}{{P}_{\mathrm{1}} {P}_{\mathrm{2}} {P}_{\mathrm{3}......} } \\ $$$${x}^{\mathrm{2}} =\mathrm{7}+\frac{{n}!}{\coprod{Pn}} \\ $$$${n}\Rightarrow\infty\Rightarrow\frac{{n}!}{\coprod{P}_{{n}} }\Rightarrow\mathrm{0}\:\:\:\:\:\:\therefore{x}^{\mathrm{2}} =\mathrm{7} \\ $$$$\:\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{7}} \\ $$$$\:\:\:\:\:\:{x}=\sqrt{\mathrm{7}}\:\:\:{approves} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{initial}\:{condition} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$
