
Question Number 182075 by Acem last updated on 04/Dec/22
Commented by Acem last updated on 04/Dec/22
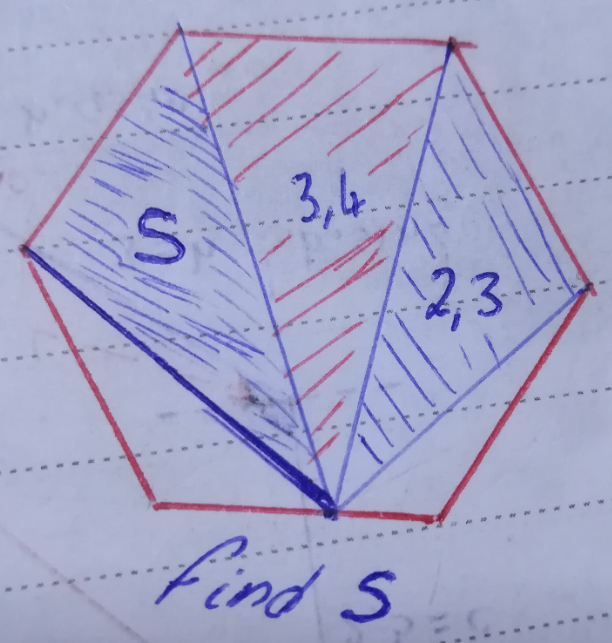
$${Regular}\:{hexagon}\:\uparrow \\ $$
Answered by mr W last updated on 04/Dec/22
Commented by mr W last updated on 04/Dec/22
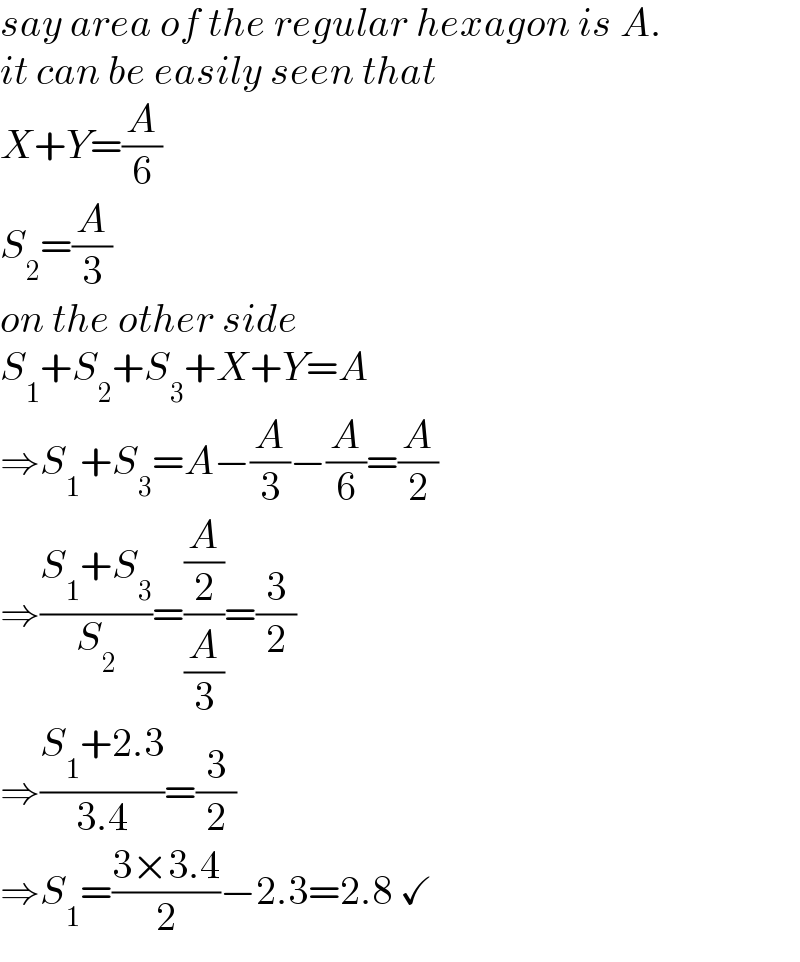
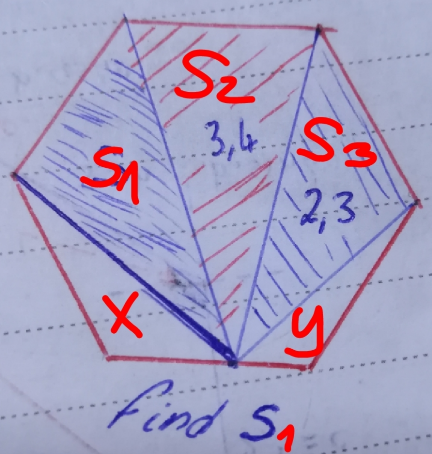
$${say}\:{area}\:{of}\:{the}\:{regular}\:{hexagon}\:{is}\:{A}. \\ $$$${it}\:{can}\:{be}\:{easily}\:{seen}\:{that} \\ $$$${X}+{Y}=\frac{{A}}{\mathrm{6}} \\ $$$${S}_{\mathrm{2}} =\frac{{A}}{\mathrm{3}}\:\: \\ $$$${on}\:{the}\:{other}\:{side} \\ $$$${S}_{\mathrm{1}} +{S}_{\mathrm{2}} +{S}_{\mathrm{3}} +{X}+{Y}={A} \\ $$$$\Rightarrow{S}_{\mathrm{1}} +{S}_{\mathrm{3}} ={A}−\frac{{A}}{\mathrm{3}}−\frac{{A}}{\mathrm{6}}=\frac{{A}}{\mathrm{2}}\:\: \\ $$$$\Rightarrow\frac{{S}_{\mathrm{1}} +{S}_{\mathrm{3}} }{{S}_{\mathrm{2}} }=\frac{\frac{{A}}{\mathrm{2}}}{\frac{{A}}{\mathrm{3}}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{S}_{\mathrm{1}} +\mathrm{2}.\mathrm{3}}{\mathrm{3}.\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow{S}_{\mathrm{1}} =\frac{\mathrm{3}×\mathrm{3}.\mathrm{4}}{\mathrm{2}}−\mathrm{2}.\mathrm{3}=\mathrm{2}.\mathrm{8}\:\checkmark \\ $$
Commented by Acem last updated on 04/Dec/22

$${Yes},\:{thanks}\:{Sir}! \\ $$
Answered by Acem last updated on 04/Dec/22

