Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 181852 by mnjuly1970 last updated on 01/Dec/22

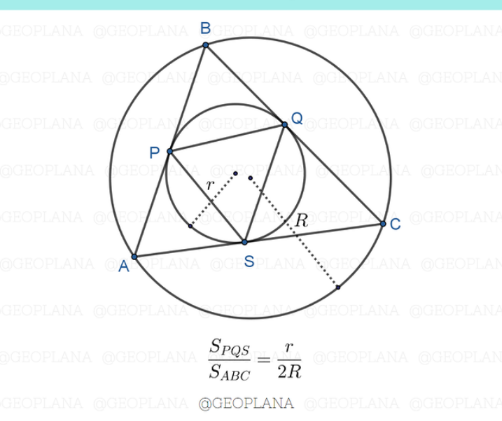
Answered by mr W last updated on 01/Dec/22

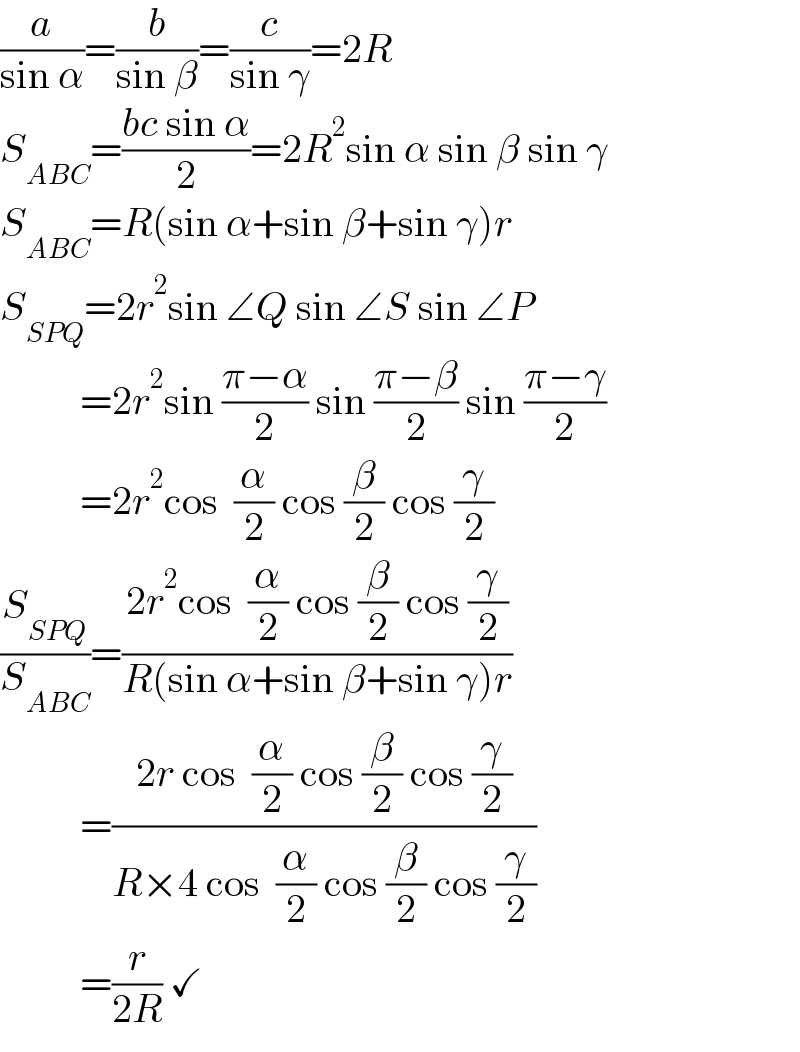
(a/(sin α))=(b/(sin β))=(c/(sin γ))=2R S_(ABC) =((bc sin α)/2)=2R^2 sin α sin β sin γ S_(ABC) =R(sin α+sin β+sin γ)r S_(SPQ) =2r^2 sin ∠Q sin ∠S sin ∠P =2r^2 sin ((π−α)/2) sin ((π−β)/2) sin ((π−γ)/2) =2r^2 cos (α/2) cos (β/2) cos (γ/2) (S_(SPQ) /S_(ABC) )=((2r^2 cos (α/2) cos (β/2) cos (γ/2))/(R(sin α+sin β+sin γ)r)) =((2r cos (α/2) cos (β/2) cos (γ/2))/(R×4 cos (α/2) cos (β/2) cos (γ/2))) =(r/(2R)) ✓

$$\frac{{a}}{\mathrm{sin}\:\alpha}=\frac{{b}}{\mathrm{sin}\:\beta}=\frac{{c}}{\mathrm{sin}\:\gamma}=\mathrm{2}{R} \\ $$$${S}_{{ABC}} =\frac{{bc}\:\mathrm{sin}\:\alpha}{\mathrm{2}}=\mathrm{2}{R}^{\mathrm{2}} \mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma \\ $$$${S}_{{ABC}} ={R}\left(\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta+\mathrm{sin}\:\gamma\right){r} \\ $$$${S}_{{SPQ}} =\mathrm{2}{r}^{\mathrm{2}} \mathrm{sin}\:\angle{Q}\:\mathrm{sin}\:\angle{S}\:\mathrm{sin}\:\angle{P} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{r}^{\mathrm{2}} \mathrm{sin}\:\frac{\pi−\alpha}{\mathrm{2}}\:\mathrm{sin}\:\frac{\pi−\beta}{\mathrm{2}}\:\mathrm{sin}\:\frac{\pi−\gamma}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}\:\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}} \\ $$$$\frac{{S}_{{SPQ}} }{{S}_{{ABC}} }=\frac{\mathrm{2}{r}^{\mathrm{2}} \mathrm{cos}\:\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}}{{R}\left(\mathrm{sin}\:\alpha+\mathrm{sin}\:\beta+\mathrm{sin}\:\gamma\right){r}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{r}\:\mathrm{cos}\:\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}}{{R}×\mathrm{4}\:\mathrm{cos}\:\:\frac{\alpha}{\mathrm{2}}\:\mathrm{cos}\:\frac{\beta}{\mathrm{2}}\:\mathrm{cos}\:\frac{\gamma}{\mathrm{2}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{{r}}{\mathrm{2}{R}}\:\checkmark \\ $$

Commented by mnjuly1970 last updated on 01/Dec/22

very nice proof ...thanks alot

$$\:\:{very}\:{nice}\:{proof}\:...{thanks}\:{alot} \\ $$

Answered by mnjuly1970 last updated on 01/Dec/22

Terms of Service

Privacy Policy

Contact: info@tinkutara.com