Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

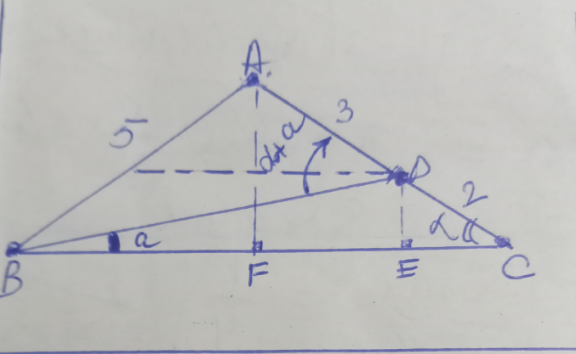
Question Number 181839 by amin96 last updated on 01/Dec/22

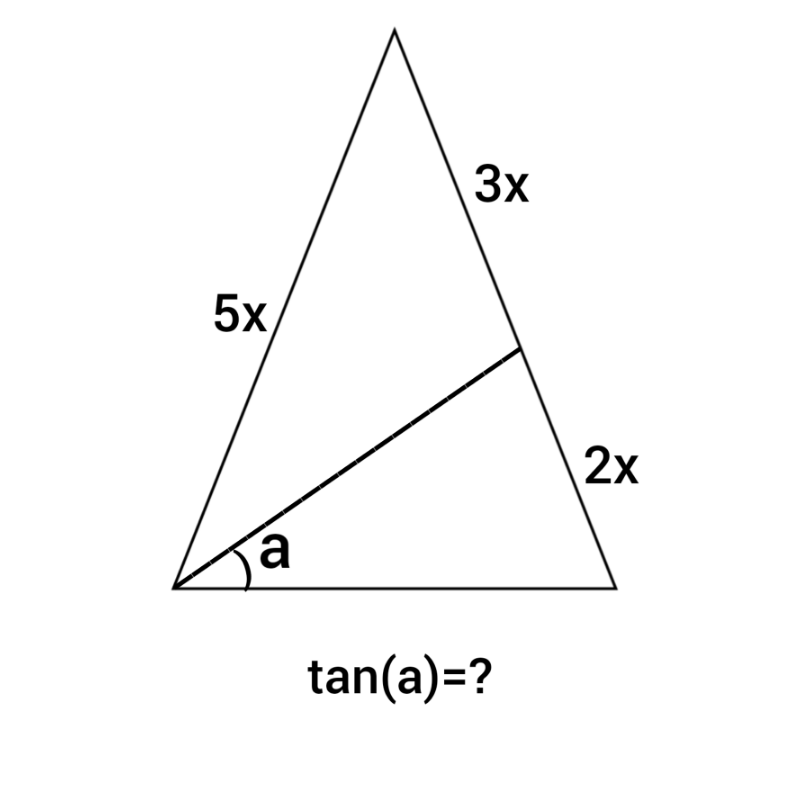
Commented by mr W last updated on 01/Dec/22

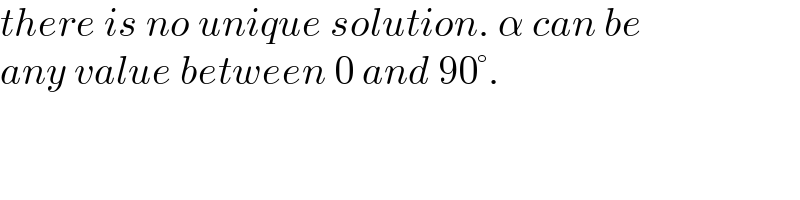
there is no unique solution. α can be any value between 0 and 90°.

$${there}\:{is}\:{no}\:{unique}\:{solution}.\:\alpha\:{can}\:{be} \\ $$$${any}\:{value}\:{between}\:\mathrm{0}\:{and}\:\mathrm{90}°. \\ $$

Commented by Acem last updated on 02/Dec/22

The intent could be to divide the side by ratio (2/3)

$${The}\:{intent}\:{could}\:{be}\:{to}\:{divide}\:{the}\:{side}\:{by}\:{ratio}\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Commented by mr W last updated on 02/Dec/22

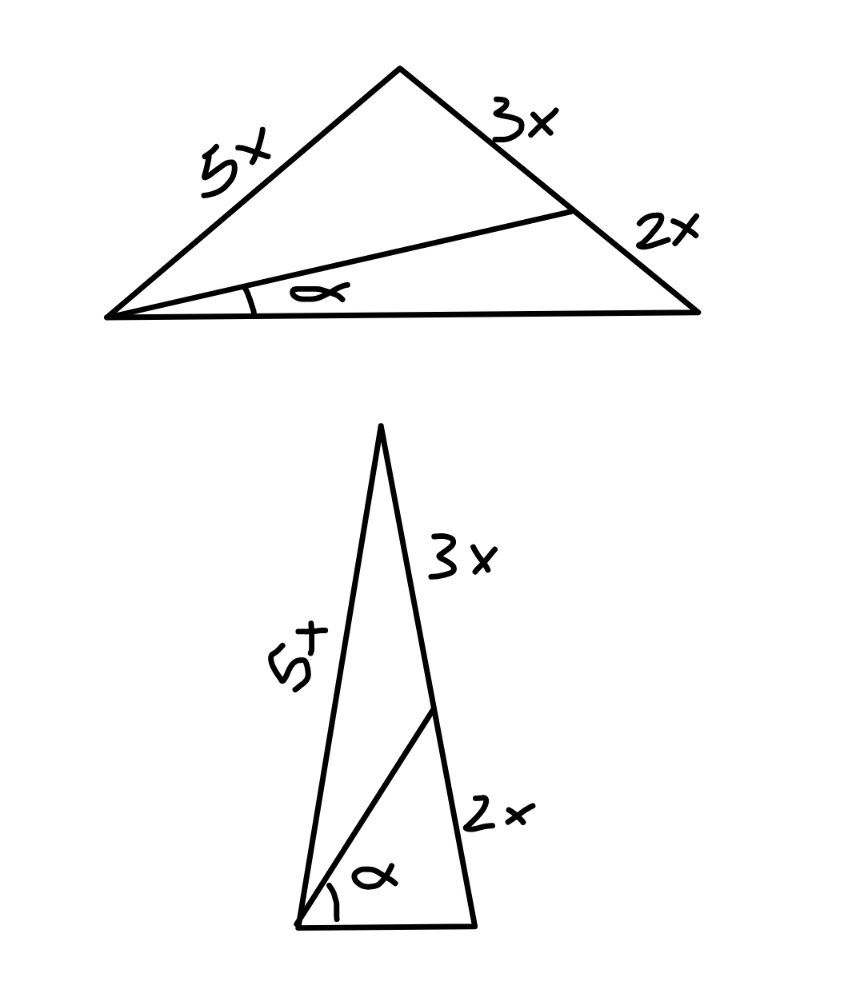
Commented by mr W last updated on 02/Dec/22

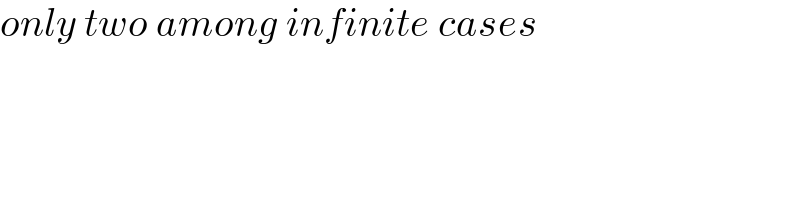
only two among infinite cases

$${only}\:{two}\:{among}\:{infinite}\:{cases} \\ $$

Commented by Acem last updated on 02/Dec/22

You′re right!

$${You}'{re}\:{right}! \\ $$

Answered by a.lgnaoui last updated on 02/Dec/22

Triangle ABD ((sin ∡ABD)/3)=((sin ∡ADB)/5)=((sin ∡BAD)/(BD)) ((sin (α−a))/3)=((sin(α+a))/5) 5sin (α−a)=3sin (α+a) 5(sin αcos a−cos αsin a)=3(sin αcos a+cos αsin a) 2sin αcos a=8cos αsin a (1/4)=tan a×cot α=((tan a)/(tan α)) (1) Triangle ABC BC^2 =AB^2 +AC^2 −2AB×ACcos 2α BC^2 =50−50cos 2α (2) tan α=((AF)/(BF))=((2×AF)/(BC)) AF=5sin α tan α=((10sin α)/(BC)) 5^2 =AF^2 +((BC^2 )/4)=5^2 sin^2 α+ 50(1−cos 2α) sin α=((AF)/5)⇒ AF=5sin α 25=25sin^2 α+((50)/4)(1−cos 2α) 1=sin^2 α+(1/2)(1−cos^2 α+sin^2 α) 1=2sin^2 α+(1/2)⇒sin α=(1/2) (α=(π/6)) tan a=((tan α)/4) =(1/(4(√3)))=((√3)/(12)) Angle a=8,21^°

$$\mathrm{Triangle}\:\mathrm{ABD}\: \\ $$$$\:\frac{\mathrm{sin}\:\measuredangle\mathrm{ABD}}{\mathrm{3}}=\frac{\mathrm{sin}\:\measuredangle\mathrm{ADB}}{\mathrm{5}}=\frac{\mathrm{sin}\:\measuredangle\mathrm{BAD}}{\mathrm{BD}} \\ $$$$\frac{\mathrm{sin}\:\left(\alpha−{a}\right)}{\mathrm{3}}=\frac{\mathrm{sin}\left(\alpha+{a}\right)}{\mathrm{5}} \\ $$$$\mathrm{5sin}\:\left(\alpha−{a}\right)=\mathrm{3sin}\:\left(\alpha+{a}\right) \\ $$$$\mathrm{5}\left(\mathrm{sin}\:\alpha\mathrm{cos}\:{a}−\mathrm{cos}\:\alpha\mathrm{sin}\:{a}\right)=\mathrm{3}\left(\mathrm{sin}\:\alpha\mathrm{cos}\:{a}+\mathrm{cos}\:\alpha\mathrm{sin}\:{a}\right) \\ $$$$\mathrm{2sin}\:\alpha\mathrm{cos}\:{a}=\mathrm{8cos}\:\alpha\mathrm{sin}\:{a} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{tan}\:{a}×\mathrm{cot}\:\alpha=\frac{\mathrm{tan}\:{a}}{\mathrm{tan}\:\alpha}\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{Triangle}\:\mathrm{ABC} \\ $$$$\mathrm{BC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{AC}^{\mathrm{2}} −\mathrm{2AB}×\mathrm{ACcos}\:\mathrm{2}\alpha \\ $$$$\:\:\:\:\mathrm{BC}^{\mathrm{2}} \:\:\:\:=\mathrm{50}−\mathrm{50cos}\:\mathrm{2}\alpha\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{AF}}{\mathrm{BF}}=\frac{\mathrm{2}×\mathrm{AF}}{\mathrm{BC}}\:\:\:\:\mathrm{AF}=\mathrm{5sin}\:\alpha \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{10sin}\:\alpha}{\mathrm{BC}} \\ $$$$\mathrm{5}^{\mathrm{2}} =\mathrm{AF}^{\mathrm{2}} +\frac{\mathrm{BC}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{5}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha+\:\mathrm{50}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$$\mathrm{sin}\:\alpha=\frac{\mathrm{AF}}{\mathrm{5}}\Rightarrow\:\:\:\mathrm{AF}=\mathrm{5sin}\:\alpha \\ $$$$\mathrm{25}=\mathrm{25sin}\:^{\mathrm{2}} \alpha+\frac{\mathrm{50}}{\mathrm{4}}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{2}\alpha\right) \\ $$$$\mathrm{1}=\mathrm{sin}\:^{\mathrm{2}} \alpha+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \alpha\right)\: \\ $$$$\mathrm{1}=\mathrm{2sin}\:^{\mathrm{2}} \alpha+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{1}}{\mathrm{2}}\:\left(\alpha=\frac{\pi}{\mathrm{6}}\right) \\ $$$$\mathrm{tan}\:{a}=\frac{\mathrm{tan}\:\alpha}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{4}\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{12}} \\ $$$$\:\:{Angle}\:{a}=\mathrm{8},\mathrm{21}^{°} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by a.lgnaoui last updated on 02/Dec/22

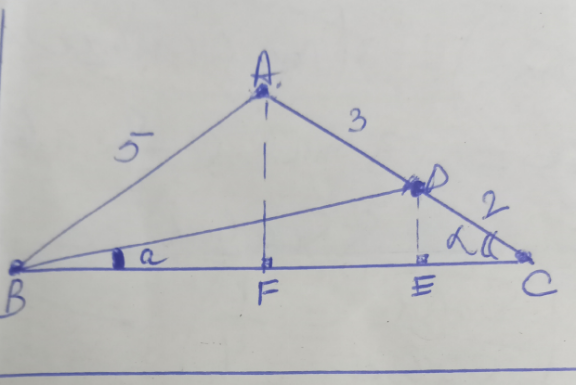
Commented by a.lgnaoui last updated on 02/Dec/22

Terms of Service

Privacy Policy

Contact: info@tinkutara.com