
Question Number 181462 by mathlove last updated on 25/Nov/22
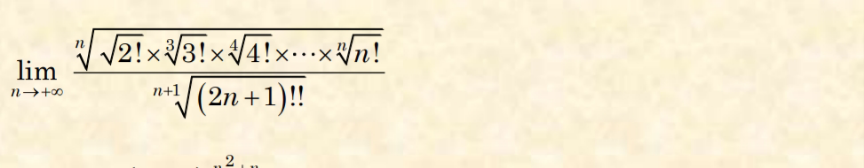
Commented by Frix last updated on 26/Nov/22

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\frac{\mathrm{1}}{\mathrm{2e}}\:\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{100\%}\:\mathrm{sure} \\ $$$$\mathrm{Can}\:\mathrm{someone}\:\mathrm{confirm}\:\mathrm{this}? \\ $$
Answered by SEKRET last updated on 25/Nov/22

$$\:\boldsymbol{\mathrm{a}}!!=\left(\mathrm{1}\centerdot\mathrm{2}\centerdot......\centerdot\boldsymbol{\mathrm{a}}\right)! \\ $$$$\:\boldsymbol{{or}} \\ $$$$\:\:\boldsymbol{\mathrm{a}}!!= \\ $$
Commented by MJS_new last updated on 25/Nov/22
![usually n!!=Π_(k=0) ^([n/2]−1) (n−2k) for n even n!!=Π_(k=1) ^(n/2) (2k) else n!!=Π_(k=1) ^((n+1)/2) (2k−1)](Q181477.png)
$$\mathrm{usually}\:{n}!!=\underset{{k}=\mathrm{0}} {\overset{\left[{n}/\mathrm{2}\right]−\mathrm{1}} {\prod}}\left({n}−\mathrm{2}{k}\right) \\ $$$$\mathrm{for}\:{n}\:\mathrm{even}\:{n}!!=\underset{{k}=\mathrm{1}} {\overset{{n}/\mathrm{2}} {\prod}}\left(\mathrm{2}{k}\right) \\ $$$$\mathrm{else}\:{n}!!=\underset{{k}=\mathrm{1}} {\overset{\left({n}+\mathrm{1}\right)/\mathrm{2}} {\prod}}\left(\mathrm{2}{k}−\mathrm{1}\right) \\ $$
Commented by MJS_new last updated on 25/Nov/22

$$\left(\mathrm{2}{n}\right)!!=\mathrm{2}^{{n}} {n}! \\ $$$$\left(\mathrm{2}{n}−\mathrm{1}\right)!!=\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{{n}} {n}!} \\ $$
Commented by SEKRET last updated on 26/Nov/22

$$\:\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{sir}}!\:\:\:\boldsymbol{\mathrm{beatiful}} \\ $$
Commented by mathlove last updated on 26/Nov/22
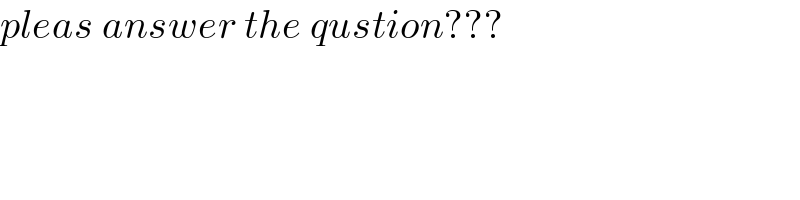
$${pleas}\:{answer}\:{the}\:{qustion}??? \\ $$
Answered by SEKRET last updated on 28/Nov/22
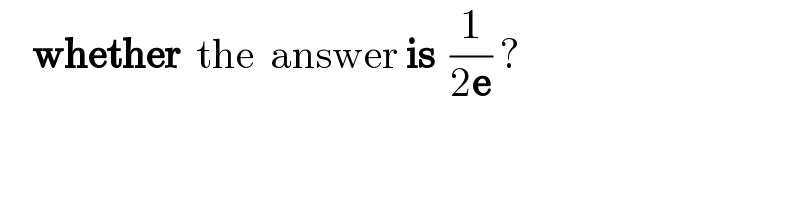
$$\:\:\:\:\boldsymbol{\mathrm{whether}}\:\:\mathrm{the}\:\:\mathrm{answer}\:\boldsymbol{\mathrm{is}}\:\:\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\mathrm{e}}}\:? \\ $$
Commented by mathlove last updated on 26/Nov/22

$${solve}\:{it}? \\ $$
