
Question Number 179631 by daus last updated on 31/Oct/22
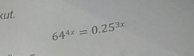
Commented by daus last updated on 31/Oct/22

$${solve}\:{for}\:{x} \\ $$
Answered by Rasheed.Sindhi last updated on 31/Oct/22

$$\mathrm{64}^{\mathrm{4}{x}} =\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}{x}} \\ $$$$\mathrm{4}^{\mathrm{12}{x}} .\mathrm{4}^{\mathrm{3}{x}} =\mathrm{1} \\ $$$$\mathrm{4}^{\mathrm{15}{x}} =\mathrm{4}^{\mathrm{0}} \\ $$$$\mathrm{15}{x}=\mathrm{0} \\ $$$${x}=\mathrm{0} \\ $$
Commented by daus last updated on 31/Oct/22

$${thanks}\: \\ $$
Answered by Acem last updated on 01/Nov/22

$$\mathrm{64}^{\mathrm{4}{x}} \:=\:\mathrm{0}.\mathrm{25}^{\mathrm{3}{x}} \\ $$$$\mathrm{12}{x}\:\mathrm{ln}\:\mathrm{4}=\:−\mathrm{3}{x}\:\mathrm{ln}\:\mathrm{4} \\ $$$$\mathrm{15}{x}\:\mathrm{ln}\:\mathrm{4}=\:\mathrm{0}\:\Rightarrow\:{x}=\mathrm{0} \\ $$
Answered by Rasheed.Sindhi last updated on 01/Nov/22
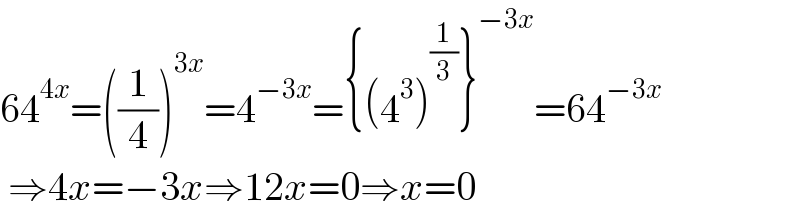
$$\mathrm{64}^{\mathrm{4}{x}} =\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}{x}} =\mathrm{4}^{−\mathrm{3}{x}} =\left\{\left(\mathrm{4}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right\}^{−\mathrm{3}{x}} =\mathrm{64}^{−\mathrm{3}{x}} \\ $$$$\:\Rightarrow\mathrm{4}{x}=−\mathrm{3}{x}\Rightarrow\mathrm{12}{x}=\mathrm{0}\Rightarrow{x}=\mathrm{0} \\ $$
