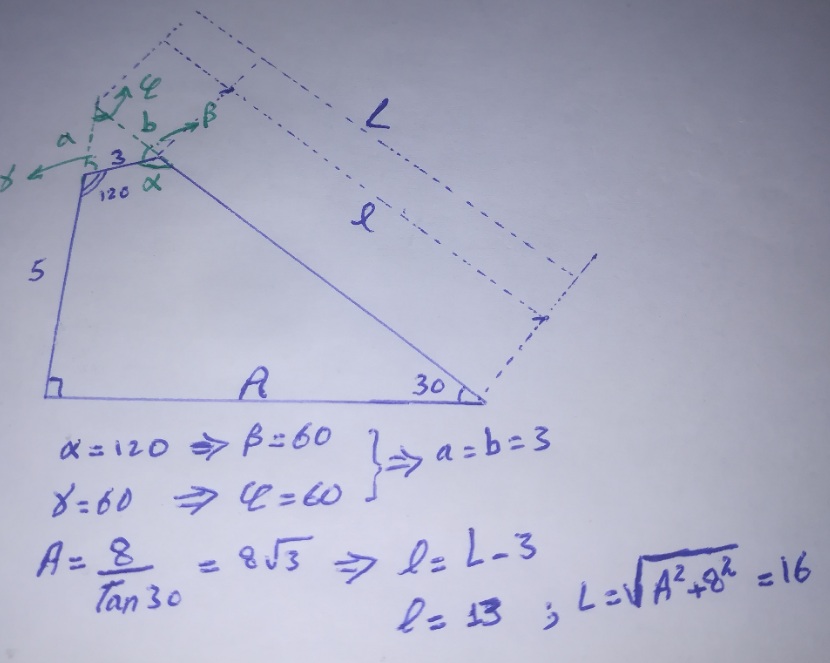
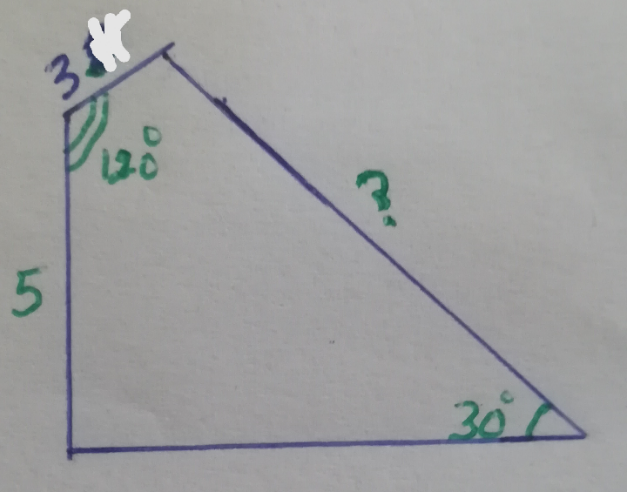
Question Number 179566 by Acem last updated on 30/Oct/22
Answered by a.lgnaoui last updated on 30/Oct/22
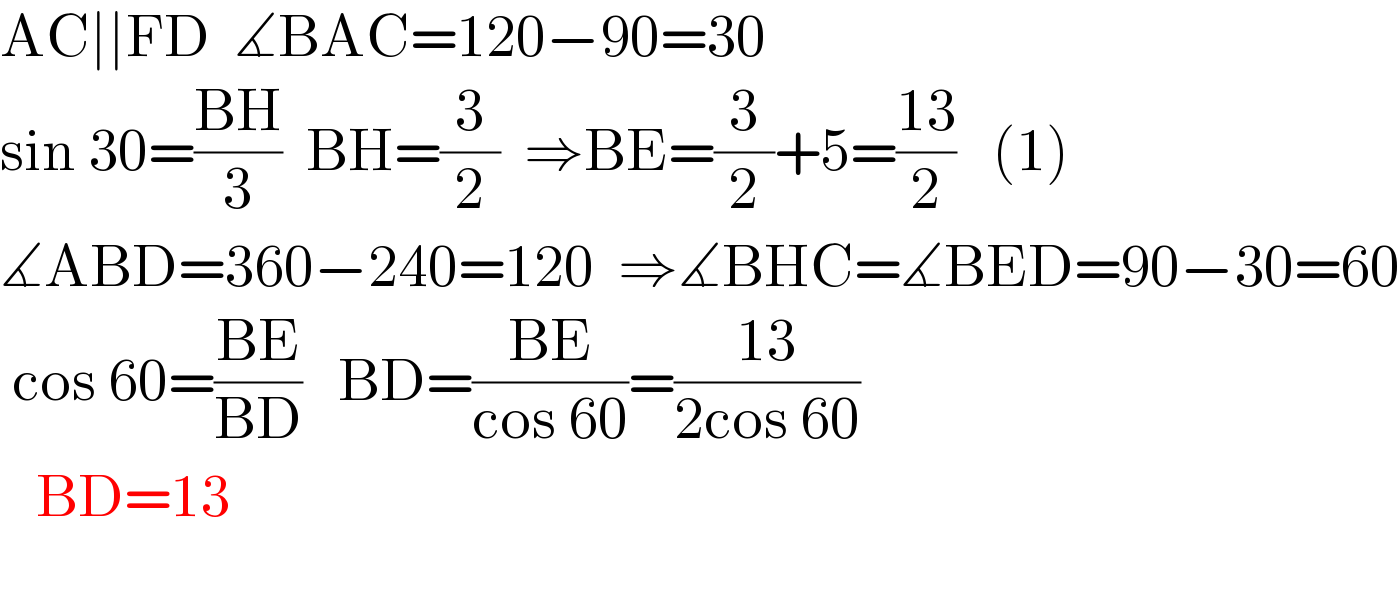
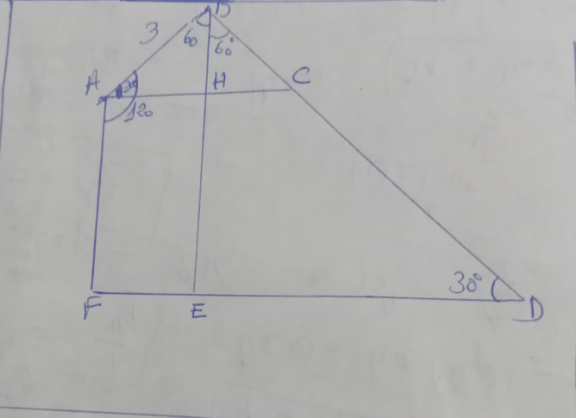
$$\mathrm{AC}\mid\mid\mathrm{FD}\:\:\measuredangle\mathrm{BAC}=\mathrm{120}−\mathrm{90}=\mathrm{30} \\ $$$$\mathrm{sin}\:\mathrm{30}=\frac{\mathrm{BH}}{\mathrm{3}}\:\:\mathrm{BH}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\Rightarrow\mathrm{BE}=\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{5}=\frac{\mathrm{13}}{\mathrm{2}}\:\:\:\left(\mathrm{1}\right) \\ $$$$\measuredangle\mathrm{ABD}=\mathrm{360}−\mathrm{240}=\mathrm{120}\:\:\Rightarrow\measuredangle\mathrm{BHC}=\measuredangle\mathrm{BED}=\mathrm{90}−\mathrm{30}=\mathrm{60} \\ $$$$\:\mathrm{cos}\:\mathrm{60}=\frac{\mathrm{BE}}{\mathrm{BD}}\:\:\:\mathrm{BD}=\frac{\mathrm{BE}}{\mathrm{cos}\:\mathrm{60}}=\frac{\mathrm{13}}{\mathrm{2cos}\:\mathrm{60}} \\ $$$$\:\:\:\mathrm{BD}=\mathrm{13} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 30/Oct/22
Commented by Acem last updated on 30/Oct/22

$${ooops}\:,\:{try}\:{again},\:{sorry} \\ $$
Commented by a.lgnaoui last updated on 30/Oct/22

$$\:\mathrm{Rectif}: \\ $$$$\measuredangle\mathrm{HBC}=\measuredangle\mathrm{EBD}=\mathrm{60}\:\:\left(\mathrm{Not}\measuredangle\:\mathrm{BHC}=\measuredangle\mathrm{BED}\right) \\ $$
Commented by Acem last updated on 30/Oct/22
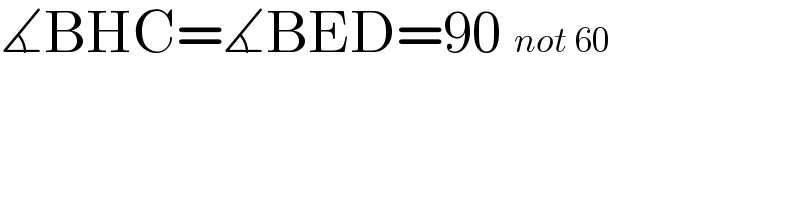
$$\measuredangle\mathrm{BHC}=\measuredangle\mathrm{BED}=\mathrm{90}\:\:{not}\:\mathrm{60} \\ $$
Commented by Acem last updated on 30/Oct/22

$${yes}\:{HBC}=\:\mathrm{60}\:,\:{you}\:{shoked}\:{me}...\:{now}\:{you}'{re}\:{right} \\ $$$$\:{And}\:{the}\:{answer}\:{is}\:{corrrrect}!\:{Thanks} \\ $$
Commented by Acem last updated on 30/Oct/22
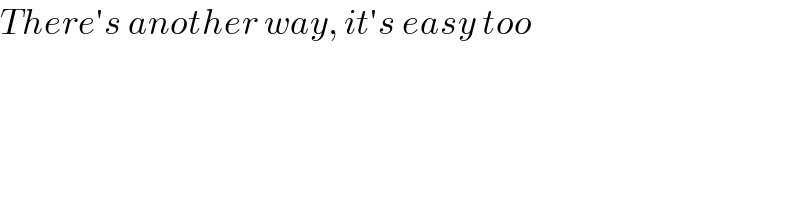
$${There}'{s}\:{another}\:{way},\:{it}'{s}\:{easy}\:{too} \\ $$
Answered by Acem last updated on 30/Oct/22