
Question Number 179440 by mr W last updated on 29/Oct/22
Commented by mr W last updated on 29/Oct/22

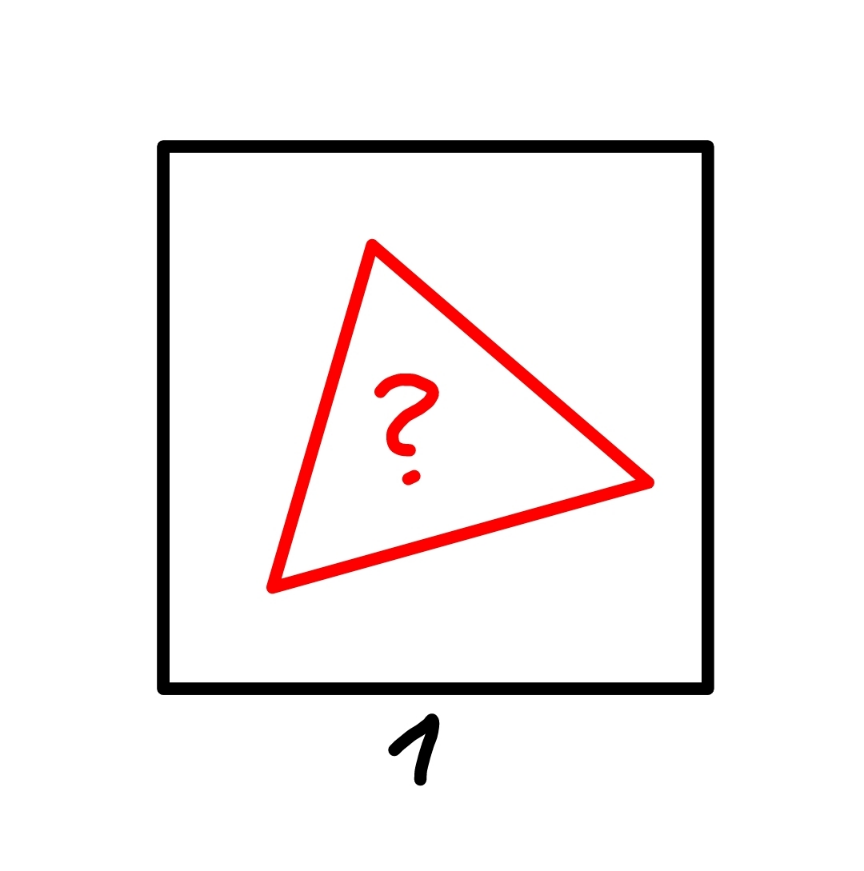
$${find}\:{the}\:{largest}\:{equilateral}\:{triangle} \\ $$$${which}\:{can}\:{be}\:{placed}\:{inside}\:{a}\:{square} \\ $$$${with}\:{side}\:{length}\:\mathrm{1}. \\ $$
Commented by Beginner last updated on 29/Oct/22

$${Approx}\:\mathrm{1}.\mathrm{0353} \\ $$
Commented by nikif99 last updated on 29/Oct/22
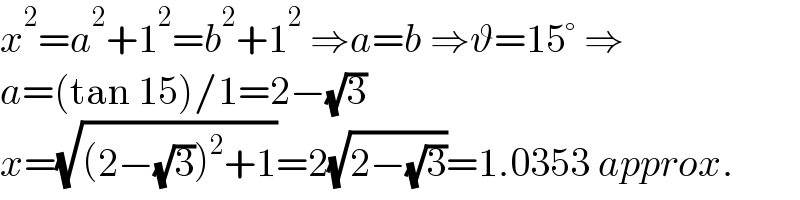
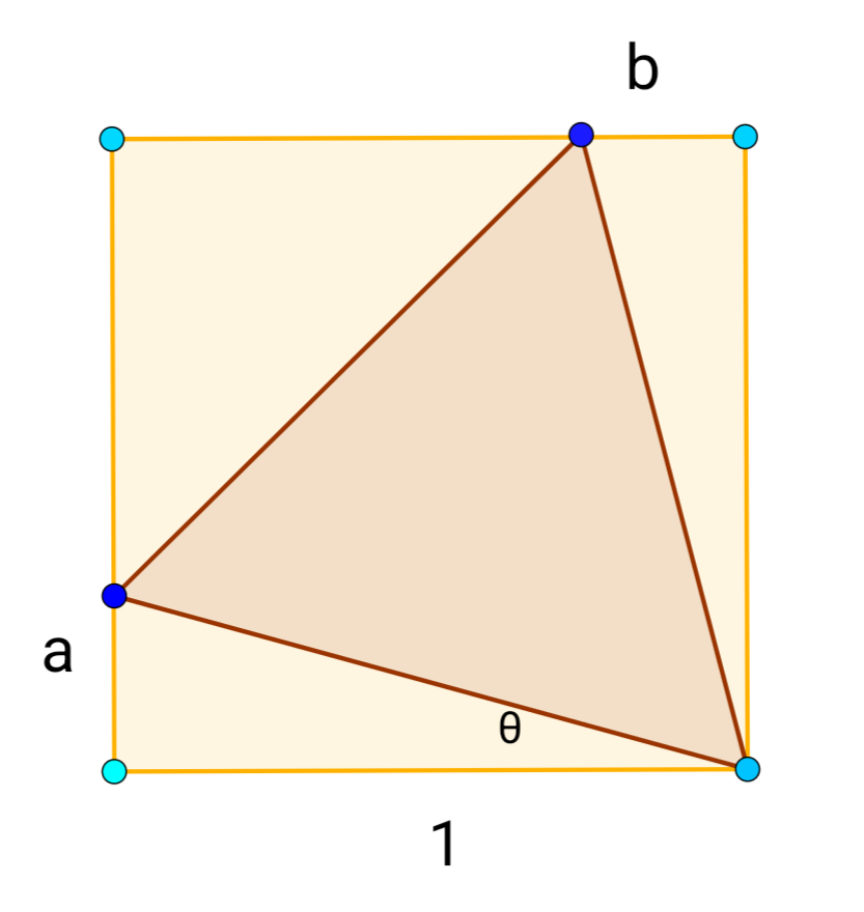
$${x}^{\mathrm{2}} ={a}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} ={b}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} \:\Rightarrow{a}={b}\:\Rightarrow\vartheta=\mathrm{15}°\:\Rightarrow \\ $$$${a}=\left(\mathrm{tan}\:\mathrm{15}\right)/\mathrm{1}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${x}=\sqrt{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}=\mathrm{1}.\mathrm{0353}\:{approx}. \\ $$
Commented by nikif99 last updated on 29/Oct/22
Commented by mr W last updated on 29/Oct/22

$${thanks}\:{sirs}! \\ $$
