
Question Number 179435 by Tawa11 last updated on 29/Oct/22
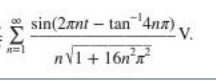
Commented by a.lgnaoui last updated on 29/Oct/22

$$\mathrm{V}? \\ $$
Answered by Peace last updated on 31/Oct/22

$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left(\mathrm{2}\pi{nt}\right){cos}\left({tan}^{−} \left(\mathrm{4}{n}\pi\right)\right)−{cos}\left(\mathrm{2}\pi{nt}\right){sin}\left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{4}{n}\pi\right)\right)}{{n}\sqrt{\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} }}={S}\left({t}\right) \\ $$$${S}\left({t}\right)={A}−{B};{A}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left(\mathrm{2}\pi{nt}\right).\sqrt{\frac{\mathrm{1}}{\mathrm{1}+{tg}^{\mathrm{2}} \left(\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{4}{n}\pi\right)\right)}}}{{n}\sqrt{\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} }} \\ $$$${B}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}\pi{nt}\right).\sqrt{\frac{{tg}^{\mathrm{2}} \left({tan}^{−} \left(\mathrm{4}{n}\pi\right)\right)}{\mathrm{1}+{tg}^{\mathrm{2}} \left({tan}^{−} \left(\mathrm{4}\boldsymbol{{n}\pi}\right)\right)}}}{{n}\sqrt{\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} }} \\ $$$$=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{cos}\left(\mathrm{2}\pi{nt}\right)\mathrm{4}\pi}{\:\left(\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)}={Re}\Sigma\frac{{e}^{\mathrm{2}{in}\pi{t}} .\mathrm{4}\pi}{\left(\mathrm{4}{n}\pi+{i}\right)\left(\mathrm{4}{n}\pi−{i}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}\pi}\Sigma\left(\frac{{e}^{\mathrm{2}{in}\pi{t}} }{{n}−\frac{{i}}{\mathrm{4}\pi}}\:−\:\:\:\:\frac{{e}^{\mathrm{2}{in}\pi{t}} }{{n}+\frac{{i}}{\mathrm{4}\pi}}\right) \\ $$$${A}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{sin}\left(\mathrm{2}\pi{nt}\right)}{{n}\left(\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)}={Im}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{e}^{{i}\mathrm{2}\pi{nt}} }{{n}\left(\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)} \\ $$$$\frac{\mathrm{1}}{{n}\left(\mathrm{1}+\mathrm{16}{n}^{\mathrm{2}} \pi^{\mathrm{2}} \right)}=\frac{\mathrm{1}}{{n}\left(\mathrm{4}{n}\pi−\boldsymbol{{i}}\right)\left(\mathrm{4}\boldsymbol{{n}\pi}+{i}\right)}=\frac{\mathrm{1}}{{n}}+\frac{−\mathrm{2}\pi}{\left(\mathrm{4}{n}\pi−{i}\right)}.−\frac{\mathrm{2}\pi}{\mathrm{4}{n}\pi+{i}} \\ $$$${A}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{e}^{{i}\mathrm{2}\pi{nt}} }{{n}}−\frac{\mathrm{1}}{\mathrm{2}\pi}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{e}^{\mathrm{2}{in}\pi{t}} }{{n}−\frac{{i}}{\mathrm{4}\pi}}−\frac{\mathrm{1}}{\mathrm{2}\pi}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{e}^{{i}\mathrm{2}{n}\pi{t}} }{{n}+\frac{{i}}{\mathrm{4}\pi}} \\ $$$$−{ln}\left(\mathrm{1}−{x}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{x}^{{n}} }{{n}} \\ $$$$\Phi\left({z},{s},{a}\right)=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{z}^{{n}} }{\left({n}+{a}\right)^{{s}} }\:\:{Lerch}\:{Transcendent}\:\:{Function} \\ $$$$=−{ln}\left(\mathrm{1}−{e}^{\mathrm{2}{i}\pi{nt}} \right)−\frac{\mathrm{1}}{\mathrm{2}\pi}\left(\Phi\left({e}^{\mathrm{2}{i}\pi{t}} ,\mathrm{1},−\frac{{i}}{\mathrm{4}\pi}\right)+\Phi\left({e}^{\mathrm{2}{i}\pi{t}} ,\mathrm{1},\frac{{i}}{\mathrm{4}\pi}\right)\right)={A} \\ $$$${B}=−\frac{\mathrm{1}}{\mathrm{2}\boldsymbol{\pi}}.\left(\Phi\left({e}^{\mathrm{2}{i}\pi{t}} ,\mathrm{1},−\frac{{i}}{\mathrm{4}\pi}\right)−\mathrm{8}\pi−\Phi\left({e}^{\mathrm{2}{i}\pi{t}} ,\mathrm{1},\frac{{i}}{\mathrm{4}\pi}\right)\right) \\ $$$${S}=−{Re}\left({B}\right)+{Im}\left({A}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa11 last updated on 01/Nov/22

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mindispower last updated on 02/Nov/22

$${withe}\:{pleasur}\:{thanl}\:{you}\:{all}\:{happinesse}\:{for}\:{you} \\ $$
