Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 179095 by SAMIRA last updated on 24/Oct/22

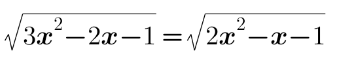
Commented by HeferH last updated on 24/Oct/22

x_1 =1; x_2 =0

$${x}_{\mathrm{1}} =\mathrm{1};\:{x}_{\mathrm{2}} =\mathrm{0}\: \\ $$$$\: \\ $$

Answered by aleks041103 last updated on 24/Oct/22

3x^2 −2x−1≥0 (x−1)(3x+1)≥0⇒x∈(−∞,−(1/3)]∪[1,∞) 2x^2 −x−1≥0 (x−1)(2x+1)≥0⇒x∈(−∞,−(1/2)]∪[1,∞) both must be satisfied ⇒x∈(−∞,−(1/2)]∪[1,∞) then 3x^2 −2x−1=2x^2 −x−1 x^2 −x=0⇒x=0,1 ⇒only ans. x=1

$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{3}{x}+\mathrm{1}\right)\geqslant\mathrm{0}\Rightarrow{x}\in\left(−\infty,−\frac{\mathrm{1}}{\mathrm{3}}\right]\cup\left[\mathrm{1},\infty\right) \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)\geqslant\mathrm{0}\Rightarrow{x}\in\left(−\infty,−\frac{\mathrm{1}}{\mathrm{2}}\right]\cup\left[\mathrm{1},\infty\right) \\ $$$${both}\:{must}\:{be}\:{satisfied} \\ $$$$\Rightarrow{x}\in\left(−\infty,−\frac{\mathrm{1}}{\mathrm{2}}\right]\cup\left[\mathrm{1},\infty\right) \\ $$$${then} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}=\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{x}=\mathrm{0}\Rightarrow{x}=\mathrm{0},\mathrm{1} \\ $$$$\Rightarrow{only}\:{ans}.\:{x}=\mathrm{1} \\ $$

Commented by Frix last updated on 24/Oct/22

why 3x^2 −2x−1≥0? there′s no restriction saying both sides of the given equation must be real numbers ⇒ x=0 is a solution because (√(−1))=(√(−1))

$$\mathrm{why}\:\mathrm{3}{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{1}\geqslant\mathrm{0}? \\ $$$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{restriction}\:\mathrm{saying}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{must}\:\mathrm{be}\:\mathrm{real}\:\mathrm{numbers} \\ $$$$\Rightarrow \\ $$$${x}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{because}\:\sqrt{−\mathrm{1}}=\sqrt{−\mathrm{1}} \\ $$

Commented by Acem last updated on 25/Oct/22

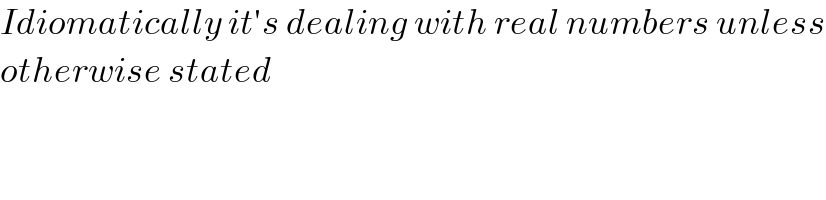
Idiomatically it′s dealing with real numbers unless otherwise stated

$${Idiomatically}\:{it}'{s}\:{dealing}\:{with}\:{real}\:{numbers}\:{unless} \\ $$$${otherwise}\:{stated} \\ $$$$ \\ $$

Commented by Acem last updated on 25/Oct/22

Good Sir!

$${Good}\:{Sir}! \\ $$

Commented by MJS_new last updated on 25/Oct/22

for me everything is dealing with complex numbers unless otherwise stated.

$$\mathrm{for}\:\mathrm{me}\:\mathrm{everything}\:\mathrm{is}\:\mathrm{dealing}\:\mathrm{with}\:\mathrm{complex} \\ $$$$\mathrm{numbers}\:\mathrm{unless}\:\mathrm{otherwise}\:\mathrm{stated}. \\ $$

Answered by Acem last updated on 25/Oct/22

x= 0 ∉ I Refused , x= 1 ∈ I ; The common domain is I= ]−∞, −(1/2)] ∪ [1, +∞[

$$\:{x}=\:\mathrm{0}\:\notin\:{I}\:{Refused}\:\:,\:\boldsymbol{{x}}=\:\mathrm{1}\:\in\:{I}\:; \\ $$$$\left.{T}\left.{he}\:{common}\:{domain}\:{is}\:{I}=\:\right]−\infty,\:−\frac{\mathrm{1}}{\mathrm{2}}\right]\:\cup\:\left[\mathrm{1},\:+\infty\left[\right.\right. \\ $$$$ \\ $$

Commented by MJS_new last updated on 25/Oct/22

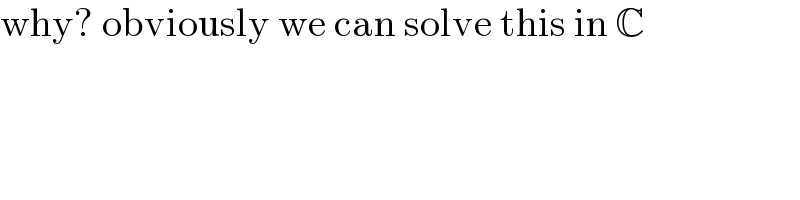
why? obviously we can solve this in C

$$\mathrm{why}?\:\mathrm{obviously}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{in}\:\mathbb{C} \\ $$

Commented by Acem last updated on 25/Oct/22

Yes you can, but on the other hand, and in this case, what′s the definition set of (√x) ?

$${Yes}\:{you}\:{can},\:{but}\:{on}\:{the}\:{other}\:{hand},\:{and}\:{in}\: \\ $$$$\:{this}\:{case},\:{what}'{s}\:{the}\:{definition}\:{set}\:{of}\:\sqrt{{x}}\:? \\ $$

Commented by MJS_new last updated on 25/Oct/22

sorry but it′s like saying we cannot solve 2x+5=2 because it′s generally understood that x∈N

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{it}'\mathrm{s}\:\mathrm{like}\:\mathrm{saying}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{solve} \\ $$$$\mathrm{2}{x}+\mathrm{5}=\mathrm{2}\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{generally}\:\mathrm{understood} \\ $$$$\mathrm{that}\:{x}\in\mathbb{N} \\ $$

Commented by Acem last updated on 25/Oct/22

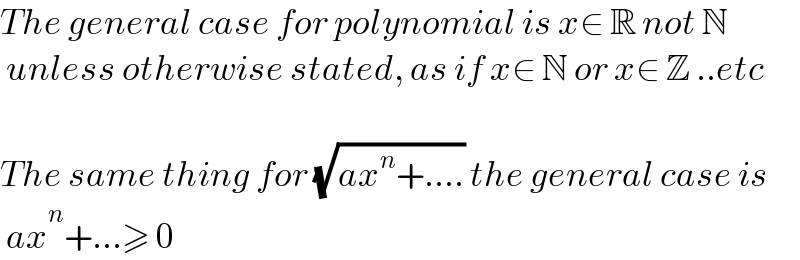
The general case for polynomial is x∈ R not N unless otherwise stated, as if x∈ N or x∈ Z ..etc The same thing for (√(ax^n +....)) the general case is ax^n +...≥ 0

$${The}\:{general}\:{case}\:{for}\:{polynomial}\:{is}\:{x}\in\:\mathbb{R}\:{not}\:\mathbb{N} \\ $$$$\:{unless}\:{otherwise}\:{stated},\:{as}\:{if}\:{x}\in\:\mathbb{N}\:{or}\:{x}\in\:\mathbb{Z}\:..{etc} \\ $$$$ \\ $$$${The}\:{same}\:{thing}\:{for}\:\sqrt{{ax}^{{n}} +....}\:{the}\:{general}\:{case}\:{is} \\ $$$$\:{ax}^{{n}} +...\geqslant\:\mathrm{0} \\ $$

Commented by MJS_new last updated on 25/Oct/22

these are your rules, not general rules. it makes no sense to keep on discussing

$$\mathrm{these}\:\mathrm{are}\:{your}\:\mathrm{rules},\:\mathrm{not}\:\mathrm{general}\:\mathrm{rules}.\:\mathrm{it}\:\mathrm{makes} \\ $$$$\mathrm{no}\:\mathrm{sense}\:\mathrm{to}\:\mathrm{keep}\:\mathrm{on}\:\mathrm{discussing} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com