Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 179064 by HeferH last updated on 24/Oct/22

Commented by HeferH last updated on 24/Oct/22

is this correct?

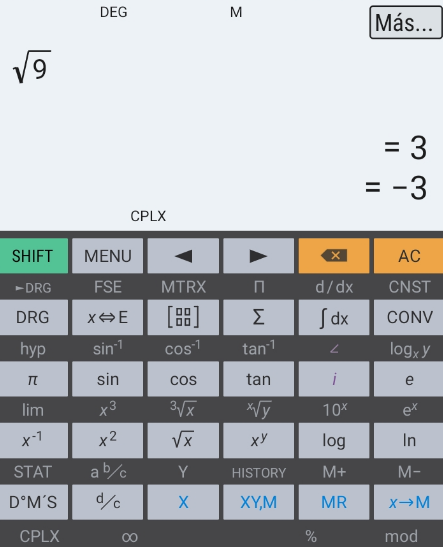
$${is}\:{this}\:{correct}? \\ $$

Commented by Rasheed.Sindhi last updated on 24/Oct/22

I think it depends upon ′notation′: if we decide “(√( ))” denotes both roots then it may be correct.(The Hiper calculators decided this) But on the other hand our notebook math don′t accept this convention. According to our common math (that I have called here ′notebook math′): (√9) =3, −(√9) =−3 & ±(√9) = { (( 3)),((−3)) :}

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{depends}\:\mathrm{upon}\:'\mathrm{notation}': \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{decide}\:``\sqrt{\:\:\:\:}''\:\mathrm{denotes}\:\mathrm{both}\:\mathrm{roots} \\ $$$$\mathrm{then}\:\mathrm{it}\:\mathrm{may}\:\mathrm{be}\:\mathrm{correct}.\left(\mathrm{The}\:\mathrm{Hiper}\right. \\ $$$$\left.\mathrm{calculators}\:\mathrm{decided}\:\mathrm{this}\right) \\ $$$$\mathrm{But}\:\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand}\:\mathrm{our}\:\mathrm{notebook} \\ $$$$\mathrm{math}\:\mathrm{don}'\mathrm{t}\:\mathrm{accept}\:\mathrm{this}\:\mathrm{convention}. \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{our}\:\mathrm{common}\:\mathrm{math}\:\left(\mathrm{that}\right. \\ $$$$\left.\mathrm{I}\:\mathrm{have}\:\mathrm{called}\:\mathrm{here}\:'\mathrm{notebook}\:\mathrm{math}'\right): \\ $$$$\sqrt{\mathrm{9}}\:=\mathrm{3},\:−\sqrt{\mathrm{9}}\:=−\mathrm{3}\:\&\:\pm\sqrt{\mathrm{9}}\:=\begin{cases}{\:\:\:\:\mathrm{3}}\\{−\mathrm{3}}\end{cases} \\ $$

Commented by MJS_new last updated on 24/Oct/22

not correct. it doesn′t fit other rules. ∣a+bi∣≥0 for any numbers a, b ∈R ∣a+bi∣=(√(a^2 +b^2 )) ⇒ (√(a^2 +b^2 ))≥0 we do not solve an equation here, we simply follow this rule: z=re^(iθ) with r≥0∧−π≤θ<π ⇒ (√z)=(√r)e^(i(θ/2)) (z)^(1/3) =(r)^(1/3) e^(i(θ/3)) ... it′s a calculation but if we have to solve x^2 =4 we ask for all possible x which give 4 when squared since a few years this seems to get confused even by math teachers, not sure why... if (√4)=±2 how can you determine (√4)+(√4)=r you must get r_1 =−4 r_2 =0 r_3 =+4

$$\mathrm{not}\:\mathrm{correct}.\:\mathrm{it}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{fit}\:\mathrm{other}\:\mathrm{rules}. \\ $$$$\mid{a}+{b}\mathrm{i}\mid\geqslant\mathrm{0}\:\mathrm{for}\:\mathrm{any}\:\mathrm{numbers}\:{a},\:{b}\:\in\mathbb{R} \\ $$$$\mid{a}+{b}\mathrm{i}\mid=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:\Rightarrow\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\geqslant\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{not}\:\mathrm{solve}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{here},\:\mathrm{we}\:\mathrm{simply} \\ $$$$\mathrm{follow}\:\mathrm{this}\:\mathrm{rule}: \\ $$$${z}={r}\mathrm{e}^{\mathrm{i}\theta} \:\mathrm{with}\:{r}\geqslant\mathrm{0}\wedge−\pi\leqslant\theta<\pi \\ $$$$\Rightarrow \\ $$$$\sqrt{{z}}=\sqrt{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{2}}} \\ $$$$\sqrt[{\mathrm{3}}]{{z}}=\sqrt[{\mathrm{3}}]{{r}}\mathrm{e}^{\mathrm{i}\frac{\theta}{\mathrm{3}}} \\ $$$$... \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{calculation} \\ $$$$\mathrm{but}\:\mathrm{if}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{solve} \\ $$$${x}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{we}\:\mathrm{ask}\:\mathrm{for}\:\mathrm{all}\:\mathrm{possible}\:{x}\:\mathrm{which}\:\mathrm{give}\:\mathrm{4}\:\mathrm{when} \\ $$$$\mathrm{squared} \\ $$$$\mathrm{since}\:\mathrm{a}\:\mathrm{few}\:\mathrm{years}\:\mathrm{this}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{get}\:\mathrm{confused} \\ $$$$\mathrm{even}\:\mathrm{by}\:\mathrm{math}\:\mathrm{teachers},\:\mathrm{not}\:\mathrm{sure}\:\mathrm{why}... \\ $$$$\mathrm{if}\:\sqrt{\mathrm{4}}=\pm\mathrm{2}\:\mathrm{how}\:\mathrm{can}\:\mathrm{you}\:\mathrm{determine} \\ $$$$\sqrt{\mathrm{4}}+\sqrt{\mathrm{4}}={r} \\ $$$$\mathrm{you}\:\mathrm{must}\:\mathrm{get}\:{r}_{\mathrm{1}} =−\mathrm{4}\:{r}_{\mathrm{2}} =\mathrm{0}\:{r}_{\mathrm{3}} =+\mathrm{4} \\ $$

Answered by thenxtkvng last updated on 24/Oct/22

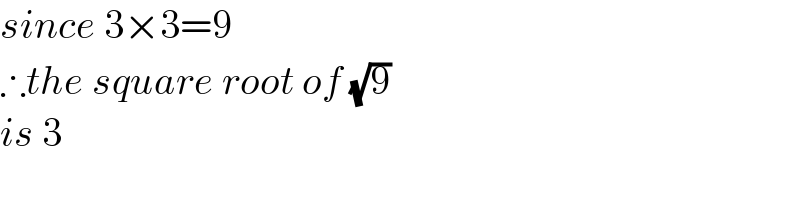
since 3×3=9 ∴the square root of (√9) is 3

$${since}\:\mathrm{3}×\mathrm{3}=\mathrm{9} \\ $$$$\therefore{the}\:{square}\:{root}\:{of}\:\sqrt{\mathrm{9}} \\ $$$${is}\:\mathrm{3} \\ $$

Commented by MJS_new last updated on 24/Oct/22

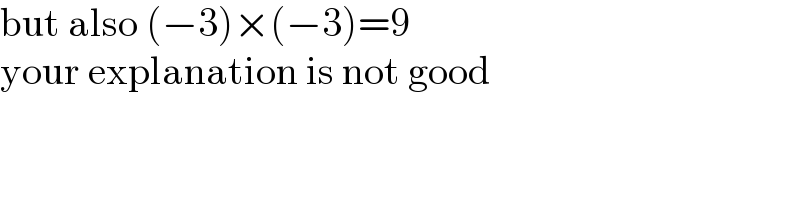
but also (−3)×(−3)=9 your explanation is not good

$$\mathrm{but}\:\mathrm{also}\:\left(−\mathrm{3}\right)×\left(−\mathrm{3}\right)=\mathrm{9} \\ $$$$\mathrm{your}\:\mathrm{explanation}\:\mathrm{is}\:\mathrm{not}\:\mathrm{good} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com