
Question Number 179053 by Giantyusuf last updated on 24/Oct/22
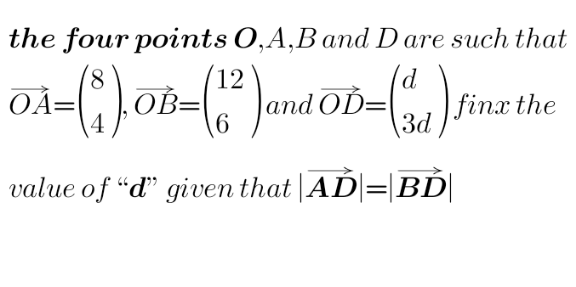
Answered by Tokugami last updated on 27/Oct/22
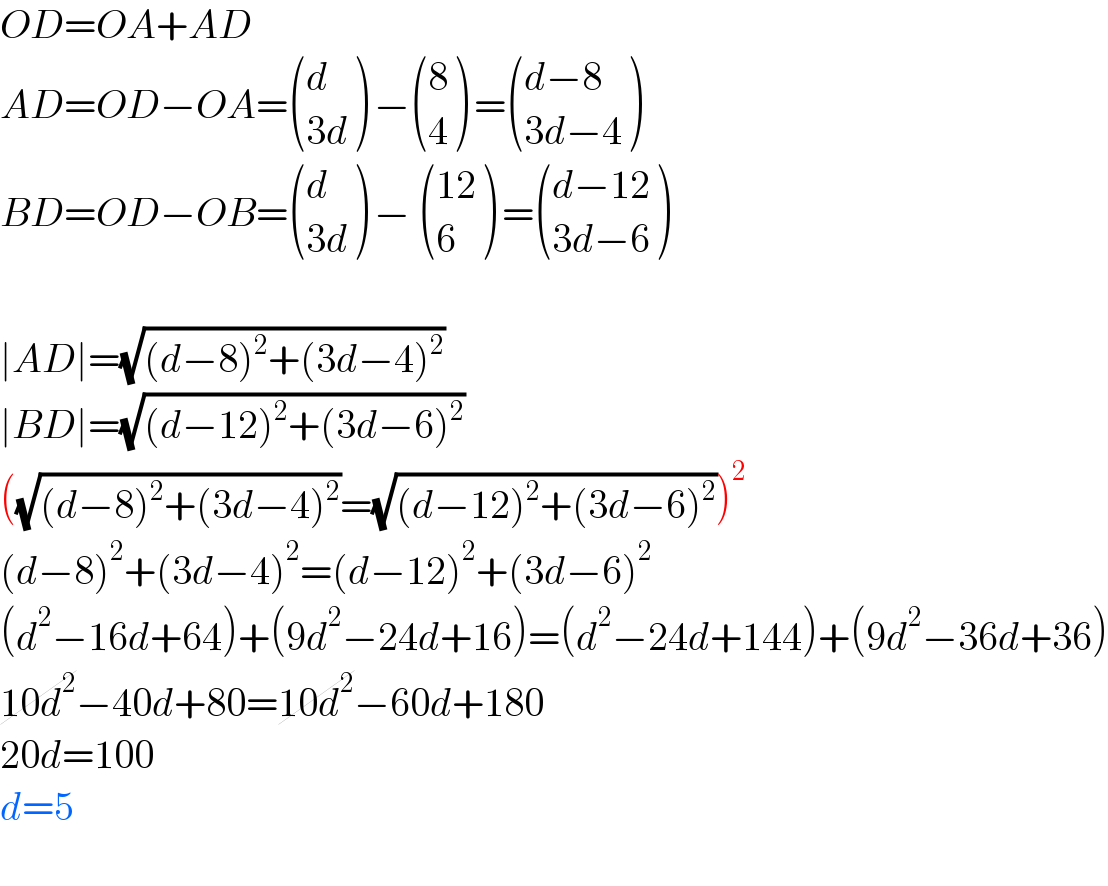
$${OD}={OA}+{AD} \\ $$$${AD}={OD}−{OA}=\begin{pmatrix}{{d}}\\{\mathrm{3}{d}}\end{pmatrix}\:−\begin{pmatrix}{\mathrm{8}}\\{\mathrm{4}}\end{pmatrix}\:=\begin{pmatrix}{{d}−\mathrm{8}}\\{\mathrm{3}{d}−\mathrm{4}}\end{pmatrix} \\ $$$${BD}={OD}−{OB}=\begin{pmatrix}{{d}}\\{\mathrm{3}{d}}\end{pmatrix}\:−\:\begin{pmatrix}{\mathrm{12}}\\{\mathrm{6}}\end{pmatrix}\:=\begin{pmatrix}{{d}−\mathrm{12}}\\{\mathrm{3}{d}−\mathrm{6}}\end{pmatrix} \\ $$$$ \\ $$$$\mid{AD}\mid=\sqrt{\left({d}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$\mid{BD}\mid=\sqrt{\left({d}−\mathrm{12}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{6}\right)^{\mathrm{2}} } \\ $$$$\left(\sqrt{\left({d}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{4}\right)^{\mathrm{2}} }=\sqrt{\left({d}−\mathrm{12}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{6}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\left({d}−\mathrm{8}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{4}\right)^{\mathrm{2}} =\left({d}−\mathrm{12}\right)^{\mathrm{2}} +\left(\mathrm{3}{d}−\mathrm{6}\right)^{\mathrm{2}} \\ $$$$\left({d}^{\mathrm{2}} −\mathrm{16}{d}+\mathrm{64}\right)+\left(\mathrm{9}{d}^{\mathrm{2}} −\mathrm{24}{d}+\mathrm{16}\right)=\left({d}^{\mathrm{2}} −\mathrm{24}{d}+\mathrm{144}\right)+\left(\mathrm{9}{d}^{\mathrm{2}} −\mathrm{36}{d}+\mathrm{36}\right) \\ $$$$\cancel{\mathrm{10}{d}^{\mathrm{2}} }−\mathrm{40}{d}+\mathrm{80}=\cancel{\mathrm{10}{d}^{\mathrm{2}} }−\mathrm{60}{d}+\mathrm{180} \\ $$$$\mathrm{20}{d}=\mathrm{100} \\ $$$${d}=\mathrm{5} \\ $$$$ \\ $$
