
Question Number 178782 by peter frank last updated on 21/Oct/22
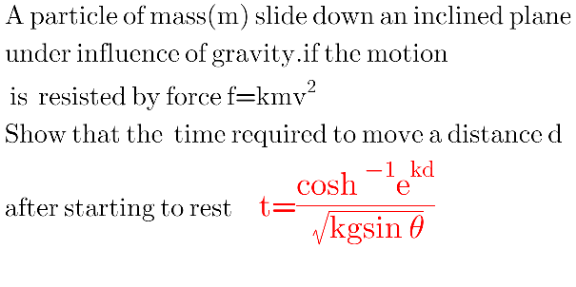
Answered by mr W last updated on 22/Oct/22
![m(dv/dt)=mg sin θ−kmv^2 dt=(dv/(g sin θ−kv^2 )) ∫_0 ^t dt=∫_0 ^v (dv/(g sin θ−kv^2 )) ∫_0 ^t dt=∫_0 ^v ((d(kv))/(((√(kg sin θ)))^2 −(kv)^2 )) t=(1/(2(√(kg sin θ))))[ln (((√(kg sin θ))+kv)/( (√(kg sin θ))−kv))]_0 ^v 2(√(kg sin θ)) t=ln (((√(kg sin θ))+kv)/( (√(kg sin θ))−kv)) e^(2(√(kg sin θ)) t) =(((√(kg sin θ))+kv)/( (√(kg sin θ))−kv)) let λ=(√(kg sin θ)) e^(2λ t) =((2λ)/( λ−kv))−1 (λ/k)(1−(2/( 1+e^(2λt) )))=v=(ds/dt) (λ/k)(1−(2/( 1+e^(2λt) )))dt=ds (λ/k)∫_0 ^t (1−(2/( 1+e^(2λt) )))dt=∫_0 ^d ds t−∫_0 ^t (2/( 1+e^(2λt) ))dt=((kd)/λ) t−(1/λ)∫_0 ^t ((d(2λt))/( 1+e^(2λt) ))=((kd)/λ) t−(1/λ)[2λt−ln (1+e^(2λt) )]_0 ^t =((kd)/λ) t−(1/λ)[2λt−ln (1+e^(2λt) )+ln 2]=((kd)/λ) t−(1/λ)ln ((2e^(2λt) )/(1+e^(2λt) ))=((kd)/λ) ln e^(λt) −ln ((2e^(2λt) )/(1+e^(2λt) ))=kd ln (((1+e^(2λt) ))/(2e^(λt) ))=kd ((1+e^(2λt) )/(2e^(λt) ))=e^(kd) (e^(λt) )^2 −2e^(kd) e^(λt) +1=0 e^(λt) =e^(kd) +(√(e^(2kd) −1)) λt=ln (e^(kd) +(√(e^(2kd) −1)))=cosh^(−1) (e^(kd) ) ⇒t=((cosh^(−1) (e^(kd) ))/λ) ⇒t=((cosh^(−1) (e^(kd) ))/( (√(kg sin θ)))) ✓](Q178852.png)
$${m}\frac{{dv}}{{dt}}={mg}\:\mathrm{sin}\:\theta−{kmv}^{\mathrm{2}} \\ $$$${dt}=\frac{{dv}}{{g}\:\mathrm{sin}\:\theta−{kv}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{{t}} {dt}=\int_{\mathrm{0}} ^{{v}} \frac{{dv}}{{g}\:\mathrm{sin}\:\theta−{kv}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{{t}} {dt}=\int_{\mathrm{0}} ^{{v}} \frac{{d}\left({kv}\right)}{\left(\sqrt{{kg}\:\mathrm{sin}\:\theta}\right)^{\mathrm{2}} −\left({kv}\right)^{\mathrm{2}} } \\ $$$${t}=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{kg}\:\mathrm{sin}\:\theta}}\left[\mathrm{ln}\:\frac{\sqrt{{kg}\:\mathrm{sin}\:\theta}+{kv}}{\:\sqrt{{kg}\:\mathrm{sin}\:\theta}−{kv}}\right]_{\mathrm{0}} ^{{v}} \\ $$$$\mathrm{2}\sqrt{{kg}\:\mathrm{sin}\:\theta}\:{t}=\mathrm{ln}\:\frac{\sqrt{{kg}\:\mathrm{sin}\:\theta}+{kv}}{\:\sqrt{{kg}\:\mathrm{sin}\:\theta}−{kv}} \\ $$$${e}^{\mathrm{2}\sqrt{{kg}\:\mathrm{sin}\:\theta}\:{t}} =\frac{\sqrt{{kg}\:\mathrm{sin}\:\theta}+{kv}}{\:\sqrt{{kg}\:\mathrm{sin}\:\theta}−{kv}} \\ $$$${let}\:\lambda=\sqrt{{kg}\:\mathrm{sin}\:\theta} \\ $$$${e}^{\mathrm{2}\lambda\:{t}} =\frac{\mathrm{2}\lambda}{\:\lambda−{kv}}−\mathrm{1} \\ $$$$\frac{\lambda}{{k}}\left(\mathrm{1}−\frac{\mathrm{2}}{\:\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }\right)={v}=\frac{{ds}}{{dt}} \\ $$$$\frac{\lambda}{{k}}\left(\mathrm{1}−\frac{\mathrm{2}}{\:\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }\right){dt}={ds} \\ $$$$\frac{\lambda}{{k}}\int_{\mathrm{0}} ^{{t}} \left(\mathrm{1}−\frac{\mathrm{2}}{\:\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }\right){dt}=\int_{\mathrm{0}} ^{{d}} {ds} \\ $$$${t}−\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{2}}{\:\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }{dt}=\frac{{kd}}{\lambda} \\ $$$${t}−\frac{\mathrm{1}}{\lambda}\int_{\mathrm{0}} ^{{t}} \frac{{d}\left(\mathrm{2}\lambda{t}\right)}{\:\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }=\frac{{kd}}{\lambda} \\ $$$${t}−\frac{\mathrm{1}}{\lambda}\left[\mathrm{2}\lambda{t}−\mathrm{ln}\:\left(\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} \right)\right]_{\mathrm{0}} ^{{t}} =\frac{{kd}}{\lambda} \\ $$$${t}−\frac{\mathrm{1}}{\lambda}\left[\mathrm{2}\lambda{t}−\mathrm{ln}\:\left(\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} \right)+\mathrm{ln}\:\mathrm{2}\right]=\frac{{kd}}{\lambda} \\ $$$${t}−\frac{\mathrm{1}}{\lambda}\mathrm{ln}\:\frac{\mathrm{2}{e}^{\mathrm{2}\lambda{t}} }{\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }=\frac{{kd}}{\lambda} \\ $$$$\mathrm{ln}\:{e}^{\lambda{t}} −\mathrm{ln}\:\frac{\mathrm{2}{e}^{\mathrm{2}\lambda{t}} }{\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }={kd} \\ $$$$\mathrm{ln}\:\frac{\left(\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} \right)}{\mathrm{2}{e}^{\lambda{t}} }={kd} \\ $$$$\:\frac{\mathrm{1}+{e}^{\mathrm{2}\lambda{t}} }{\mathrm{2}{e}^{\lambda{t}} }={e}^{{kd}} \\ $$$$\left({e}^{\lambda{t}} \right)^{\mathrm{2}} −\mathrm{2}{e}^{{kd}} {e}^{\lambda{t}} +\mathrm{1}=\mathrm{0} \\ $$$${e}^{\lambda{t}} ={e}^{{kd}} +\sqrt{{e}^{\mathrm{2}{kd}} −\mathrm{1}} \\ $$$$\lambda{t}=\mathrm{ln}\:\left({e}^{{kd}} +\sqrt{{e}^{\mathrm{2}{kd}} −\mathrm{1}}\right)=\mathrm{cosh}^{−\mathrm{1}} \:\left({e}^{{kd}} \right) \\ $$$$\Rightarrow{t}=\frac{\mathrm{cosh}^{−\mathrm{1}} \:\left({e}^{{kd}} \right)}{\lambda} \\ $$$$\Rightarrow{t}=\frac{\mathrm{cosh}^{−\mathrm{1}} \:\left({e}^{{kd}} \right)}{\:\sqrt{{kg}\:\mathrm{sin}\:\theta}}\:\checkmark \\ $$
Commented by mr W last updated on 22/Oct/22
Commented by Tawa11 last updated on 22/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Spillover last updated on 22/Oct/22

$$\mathrm{Excellent}\:\mathrm{solution}\:\mathrm{Mr}\:\mathrm{W} \\ $$
Commented by peter frank last updated on 22/Oct/22

$$\mathrm{thanks} \\ $$
Answered by Spillover last updated on 22/Oct/22
![F=ma −kmv^2 +mgsin θ=ma gsin θ−kv^2 =a (dv/dt)=gsin θ−kv^2 =k[(g/k)sin θ−v^2 ] dt=∫(dv/(k[(g/k)sin θ−v^2 ]))=(1/k)∫(dv/((g/k)sin θ−v^2 )) dt=(1/k)∫(dv/((g/k)sin θ−v^2 ))=(1/k)∫(dv/( (√(((g/k)sin θ)^2 ))−v^2 )) let β= (√((g/k)sin θ)) dt=(1/k)∫(dv/( (√(((g/k)sin θ)^2 ))−v^2 ))=(1/k)∫(dv/(β^2 −v^2 )) t=(1/k).(1/β)tanh^(−1) ((v/β))+A t=0 x=0 v=0 (v/β)=tanh (ktβ) v=βtanh (ktβ) v=βtanh (ktβ) (dx/dt)=βtanh (ktβ) dx=βtanh (ktβ) dt ∫_0 ^d dx=∫βtanh (ktβ) dt d=βln (([cosh (ktβ))/(kβ)) d=(1/k)ln cosh (ktβ) kd=ln cosh (ktβ) e^(kd) =cosh (ktβ) cosh^(−1) (e^(kd) )=ktβ t=(1/(kβ))cosh^(−1) (e^(kd) ) β= (√((g/k)sin θ)) t=(1/(k. (√((g/k)sin θ)) )).cosh^(−1) (e^(kd) ) t=((cosh^(−1) (e^(kd) ))/( (√(gksin θ))))](Q178886.png)
$$\mathrm{F}=\mathrm{ma} \\ $$$$−\mathrm{kmv}^{\mathrm{2}} +\mathrm{mgsin}\:\theta=\mathrm{ma} \\ $$$$\mathrm{gsin}\:\theta−\mathrm{kv}^{\mathrm{2}} =\mathrm{a} \\ $$$$\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{gsin}\:\theta−\mathrm{kv}^{\mathrm{2}} =\mathrm{k}\left[\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta−\mathrm{v}^{\mathrm{2}} \right] \\ $$$$\mathrm{dt}=\int\frac{\mathrm{dv}}{\mathrm{k}\left[\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta−\mathrm{v}^{\mathrm{2}} \right]}=\frac{\mathrm{1}}{\mathrm{k}}\int\frac{\mathrm{dv}}{\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta−\mathrm{v}^{\mathrm{2}} } \\ $$$$\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{k}}\int\frac{\mathrm{dv}}{\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta−\mathrm{v}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{k}}\int\frac{\mathrm{dv}}{\:\sqrt{\left(\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }−\mathrm{v}^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\beta=\:\sqrt{\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta}\: \\ $$$$\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{k}}\int\frac{\mathrm{dv}}{\:\sqrt{\left(\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta\right)^{\mathrm{2}} }−\mathrm{v}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{k}}\int\frac{\mathrm{dv}}{\beta^{\mathrm{2}} −\mathrm{v}^{\mathrm{2}} } \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{k}}.\frac{\mathrm{1}}{\beta}\mathrm{tanh}\:^{−\mathrm{1}} \left(\frac{\mathrm{v}}{\beta}\right)+\mathrm{A} \\ $$$$\mathrm{t}=\mathrm{0}\:\:\:\mathrm{x}=\mathrm{0}\:\:\:\:\mathrm{v}=\mathrm{0} \\ $$$$\frac{\mathrm{v}}{\beta}=\mathrm{tanh}\:\left(\mathrm{kt}\beta\right)\:\:\:\mathrm{v}=\beta\mathrm{tanh}\:\left(\mathrm{kt}\beta\right) \\ $$$$\:\:\mathrm{v}=\beta\mathrm{tanh}\:\left(\mathrm{kt}\beta\right)\:\:\:\:\:\frac{\mathrm{dx}}{\mathrm{dt}}=\beta\mathrm{tanh}\:\left(\mathrm{kt}\beta\right)\:\:\:\:\:\:\mathrm{dx}=\beta\mathrm{tanh}\:\left(\mathrm{kt}\beta\right)\:\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{d}} \mathrm{dx}=\int\beta\mathrm{tanh}\:\left(\mathrm{kt}\beta\right)\:\mathrm{dt}\:\: \\ $$$$\mathrm{d}=\beta\mathrm{ln}\:\frac{\left[\mathrm{cosh}\:\left(\mathrm{kt}\beta\right)\right.}{\mathrm{k}\beta} \\ $$$$\mathrm{d}=\frac{\mathrm{1}}{\mathrm{k}}\mathrm{ln}\:\mathrm{cosh}\:\left(\mathrm{kt}\beta\right) \\ $$$$\mathrm{kd}=\mathrm{ln}\:\mathrm{cosh}\:\left(\mathrm{kt}\beta\right) \\ $$$$\mathrm{e}^{\mathrm{kd}} =\mathrm{cosh}\:\left(\mathrm{kt}\beta\right) \\ $$$$\mathrm{cosh}\:^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{kd}} \right)=\mathrm{kt}\beta \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{k}\beta}\mathrm{cosh}\:^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{kd}} \right) \\ $$$$\beta=\:\sqrt{\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta}\: \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{k}.\:\sqrt{\frac{\mathrm{g}}{\mathrm{k}}\mathrm{sin}\:\theta}\:}.\mathrm{cosh}\:^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{kd}} \right) \\ $$$$\mathrm{t}=\frac{\mathrm{cosh}\:^{−\mathrm{1}} \left(\mathrm{e}^{\mathrm{kd}} \right)}{\:\sqrt{\mathrm{gksin}\:\theta}} \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 22/Oct/22

$$\mathrm{great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 22/Oct/22
$${we}\:{can}\:{see}\:{you}\:{are}\:{a}\:{fan}\:{of}\:{hyperbolic} \\ $$$${functions}.\:{that}'{s}\:{great}! \\ $$
