
Question Number 178508 by yaslm last updated on 17/Oct/22
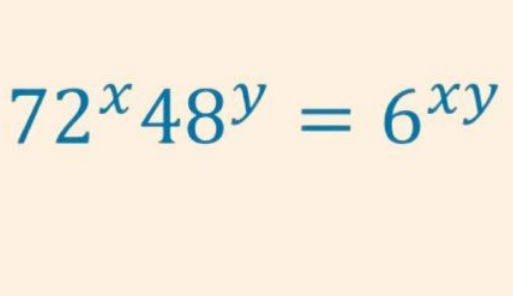
Commented by MJS_new last updated on 17/Oct/22

$$\mathrm{obviously}\:{x}={y}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{choose}\:{x}\in\mathbb{R}\backslash\left\{\mathrm{log}_{\mathrm{6}} \:\mathrm{48}\right\}\:\mathrm{to}\:\mathrm{get} \\ $$$${y}=\frac{{x}\mathrm{ln}\:\mathrm{72}}{{x}\mathrm{ln}\:\mathrm{6}\:−\mathrm{ln}\:\mathrm{48}} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:``\mathrm{nice}''\:\mathrm{solutions} \\ $$$$\mathrm{72}^{{x}} =\mathrm{2}^{\mathrm{3}{x}} \mathrm{3}^{\mathrm{2}{x}} \\ $$$$\mathrm{48}^{{y}} =\mathrm{2}^{\mathrm{4}{y}} \mathrm{3}^{{y}} \\ $$$$\mathrm{6}^{{xy}} =\mathrm{2}^{{xy}} \mathrm{3}^{{xy}} \\ $$$$\Rightarrow \\ $$$$\mathrm{2}^{\mathrm{3}{x}+\mathrm{4}{y}} \mathrm{3}^{\mathrm{2}{x}+{y}} =\mathrm{2}^{{xy}} \mathrm{3}^{{xy}} \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}={xy}\:\wedge\:\mathrm{2}{x}+{y}={xy}\:\Rightarrow\:{x}={y}=\mathrm{0}\:\vee\:{x}=−\mathrm{5}\wedge{y}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$
Answered by peter frank last updated on 17/Oct/22
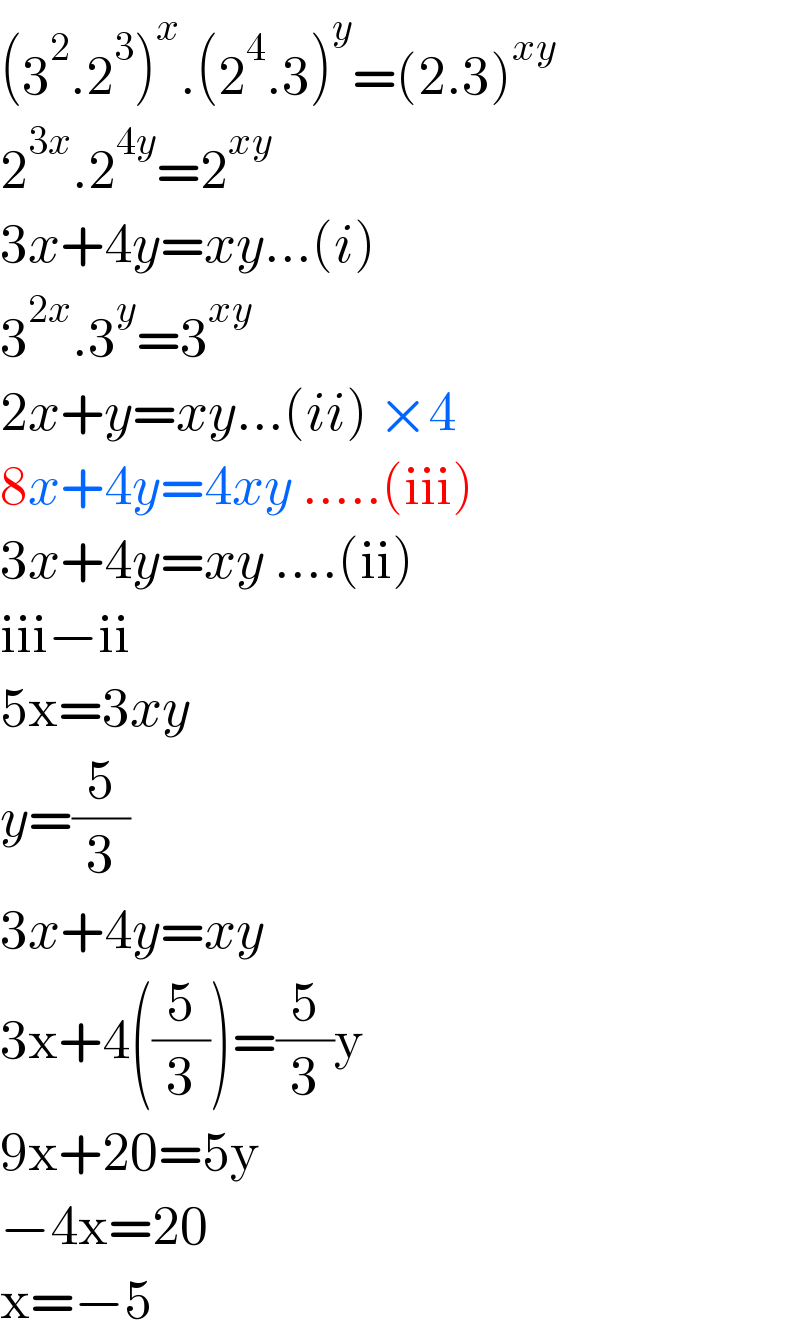
$$\left(\mathrm{3}^{\mathrm{2}} .\mathrm{2}^{\mathrm{3}} \right)^{{x}} .\left(\mathrm{2}^{\mathrm{4}} .\mathrm{3}\right)^{{y}} =\left(\mathrm{2}.\mathrm{3}\right)^{{xy}} \\ $$$$\mathrm{2}^{\mathrm{3}{x}} .\mathrm{2}^{\mathrm{4}{y}} =\mathrm{2}^{{xy}} \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}={xy}...\left({i}\right) \\ $$$$\mathrm{3}^{\mathrm{2}{x}} .\mathrm{3}^{{y}} =\mathrm{3}^{{xy}} \\ $$$$\mathrm{2}{x}+{y}={xy}...\left({ii}\right)\:×\mathrm{4} \\ $$$$\mathrm{8}{x}+\mathrm{4}{y}=\mathrm{4}{xy}\:.....\left(\mathrm{iii}\right) \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}={xy}\:....\left(\mathrm{ii}\right) \\ $$$$\mathrm{iii}−\mathrm{ii} \\ $$$$\mathrm{5x}=\mathrm{3}{xy} \\ $$$${y}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{3}{x}+\mathrm{4}{y}={xy} \\ $$$$\mathrm{3x}+\mathrm{4}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=\frac{\mathrm{5}}{\mathrm{3}}\mathrm{y} \\ $$$$\mathrm{9x}+\mathrm{20}=\mathrm{5y} \\ $$$$−\mathrm{4x}=\mathrm{20} \\ $$$$\mathrm{x}=−\mathrm{5} \\ $$
Commented by yaslm last updated on 17/Oct/22
good but try again ��
Answered by a.lgnaoui last updated on 18/Oct/22
![log(72^x x48^y )=log(6^(xy) ) xlog72+ylog48=xylog6 x((log72)/(log6))+y((log48)/(log6))=xy soit a=((log72)/(log6)) b=((log48)/(log6)) ax+by=xy xy−by=ax y(x−b)=ax y=((ax)/(x−b)) 72^x ×48^((ax)/(x−b)) =6^((ax^2 )/(x−b)) (6^x ×6^((ax)/(x−b)) )×(6×2)^x ×(8)^((ax)/(x−b)) =6^((ax^2 )/(x−b)) 6^(2x) ×2^x ×8^((ax)/(x−b)) =6^((ax^2 )/(x−b)) 2^x ×2^((3ax)/(x−b)) =6^(((ax^2 )/(x−b))−2x) 2^(x+((3ax)/(x−b))) =(2×3)^(((ax^2 )/(x−b))−2x) 2^(x+2x−((ax^2 )/(x−b))+((3ax)/(x−b))) =3^(((ax^2 )/(x−b))−2x) [3x−((ax^2 −3ax)/(x−b))]log2=[((ax^2 )/(x−b))−2x]log3 (3x^2 −3bx−ax^2 +3ax)log2=(ax^2 −2x^2 +2bx)log3 [(3−a)x^2 +3(a−b)x]log2=[(a−2)x^2 +2bx]log3 [(3−a)log2−(a−2)log3]x^2 =2b×log3−3(a−b)xlog2 x[(3−a)log2−(a−2)log3]=2b×log3−3(a−b)log2 x=((2b×log3−3(a−b)log2)/((3−a)log2−(a−2)log3)) a=((log72)/(kog6))= ((3log2+2log3)/(log2+log3)) b=((log48)/(log6))=((4log2+log3)/(log2+log3)) [a−b=((log3−log2)/(log2+log3))] x=((((2(4log2+log3)/(log2+log3))log3−3log2((log3−log2)/(log2+log3)))/(3−((3log2+2log3)/(log2+log3))−(((3log2+2log3))/(log2+log3))−2)log3)) x =(((8log2log3+log^2 3−3log2×log3+3log^2 2)/(log2+log3))/((3(log2+log3)−3log2−2log3−[3log2log3+2log^2 3−2log2log3−2log^2 3])/(log2+log3))) x=((log3(5log2+log3)+3log^2 2)/(log3(1−log2))) y=((ax)/(x−b))=((log3(5log2+log3)+3log^2 2)/(log3(1−log2)((log3(5log2+log3)+3log^2 2)/1)))×(3log2+2log3) ax=((3log2+2log3)/(log2+log3))×((log3(5log2+log3)+3log^2 2))/(log3(1−log2))) ax= (((3log2+2log3)×[(5log2.log3+log^2 3+3lo^2 g2))/(log3(1−log2))) x−b=((log3(5kog2+log3)+3log^2 2)/((1−log2)log3))−((4log2+log3)/(log2+log3))= =(((log2+log3)[(log3(5log2+log3)+3log^2 2]−[(4log2+log3)(1−log2)log3)/((1−log2)(log2+log3)log3)) ((ax)/(x−b))= (((3log2+2log3)[(log3(5log2+log3)+3log^2 2))/((1−log2)))×(((1−log2)(log2+log3)log3)/((log2+log3)[log3(5log2+log3)+3log^2 2]−[(4log2+log3)(1−log2)log3]))= =(([(3log2+2log3)(5log2log3+log^2 3]+[3log^2 2log3)×log3(1−lkg2)(log2+log3)])/((1−log2)(log2+lig3)(5log2.log3+log^2 3+3log^2 2)−[4log2+log3)(1−log2)log3))= =(((3log2+2log3)(5log2log3+log^2 3)+(3oig^2 2log3)(1−log2)(log2+log3))/((1−log2)[log2+log3)(5log2log3+log^2 3+3log^2 2)−(4log2+log3)log3)])) y=(((3log2+2log3)[log3(5log2+log3)+3log^2 2])/(log3[5log2+log3)+3log^2 2)(log3(1−log2)−(4log2log3+log^2 3))) y=(([2log^3 3+9.log^3 2+(log2.log3)(3+21.log^2 2+ 10.log3)])/([(log^4 3+log^3 3−log2log3(5log^2 3+5log3+5+22log2log3)])) de plus x=0 y=0 k](Q178536.png)
$$\mathrm{log}\left(\mathrm{72}^{\mathrm{x}} \mathrm{x48}^{\mathrm{y}} \right)=\mathrm{log}\left(\mathrm{6}^{\mathrm{xy}} \right) \\ $$$$\mathrm{xlog72}+\mathrm{ylog48}=\mathrm{xylog6} \\ $$$$\mathrm{x}\frac{\mathrm{log72}}{\mathrm{log6}}+\mathrm{y}\frac{\mathrm{log48}}{\mathrm{log6}}=\mathrm{xy}\:\:\: \\ $$$$\mathrm{soit}\:\:\mathrm{a}=\frac{\mathrm{log72}}{\mathrm{log6}}\:\:\:\:\:\:\mathrm{b}=\frac{\mathrm{log48}}{\mathrm{log6}} \\ $$$$\mathrm{ax}+\mathrm{by}=\mathrm{xy}\:\: \\ $$$$\mathrm{xy}−\mathrm{by}=\mathrm{ax}\:\:\:\:\mathrm{y}\left(\mathrm{x}−\mathrm{b}\right)=\mathrm{ax} \\ $$$$\:\:\mathrm{y}=\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}} \\ $$$$\mathrm{72}^{\mathrm{x}} ×\mathrm{48}^{\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}} =\mathrm{6}^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}} \\ $$$$\left(\mathrm{6}^{\mathrm{x}} ×\mathrm{6}^{\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}} \right)×\left(\mathrm{6}×\mathrm{2}\right)^{\mathrm{x}} ×\left(\mathrm{8}\right)^{\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}} =\mathrm{6}^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}} \\ $$$$\mathrm{6}^{\mathrm{2x}} ×\mathrm{2}^{\mathrm{x}} ×\mathrm{8}^{\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}} =\mathrm{6}^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}} \\ $$$$\mathrm{2}^{\mathrm{x}} ×\mathrm{2}^{\frac{\mathrm{3ax}}{\mathrm{x}−\mathrm{b}}} =\mathrm{6}^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}−\mathrm{2x}} \\ $$$$\mathrm{2}^{\mathrm{x}+\frac{\mathrm{3ax}}{\mathrm{x}−\mathrm{b}}} =\left(\mathrm{2}×\mathrm{3}\right)^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}−\mathrm{2x}} \\ $$$$\mathrm{2}^{\mathrm{x}+\mathrm{2x}−\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}+\frac{\mathrm{3ax}}{\mathrm{x}−\mathrm{b}}} =\mathrm{3}^{\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}−\mathrm{2x}} \\ $$$$ \\ $$$$\left[\mathrm{3x}−\frac{\mathrm{ax}^{\mathrm{2}} −\mathrm{3ax}}{\mathrm{x}−\mathrm{b}}\right]\mathrm{log2}=\left[\frac{\mathrm{ax}^{\mathrm{2}} }{\mathrm{x}−\mathrm{b}}−\mathrm{2x}\right]\mathrm{log3} \\ $$$$ \\ $$$$\left(\mathrm{3x}^{\mathrm{2}} −\mathrm{3bx}−\mathrm{ax}^{\mathrm{2}} +\mathrm{3ax}\right)\mathrm{log2}=\left(\mathrm{ax}^{\mathrm{2}} −\mathrm{2x}^{\mathrm{2}} +\mathrm{2bx}\right)\mathrm{log3} \\ $$$$\:\left[\left(\mathrm{3}−\mathrm{a}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{3}\left(\mathrm{a}−\mathrm{b}\right)\mathrm{x}\right]\mathrm{log2}=\left[\left(\mathrm{a}−\mathrm{2}\right)\mathrm{x}^{\mathrm{2}} +\mathrm{2bx}\right]\mathrm{log3} \\ $$$$\:\left[\left(\mathrm{3}−\mathrm{a}\right)\mathrm{log2}−\left(\mathrm{a}−\mathrm{2}\right)\mathrm{log3}\right]\mathrm{x}^{\mathrm{2}} =\mathrm{2b}×\mathrm{log3}−\mathrm{3}\left(\mathrm{a}−\mathrm{b}\right)\mathrm{xlog2} \\ $$$$\mathrm{x}\left[\left(\mathrm{3}−\mathrm{a}\right)\mathrm{log2}−\left(\mathrm{a}−\mathrm{2}\right)\mathrm{log3}\right]=\mathrm{2b}×\mathrm{log3}−\mathrm{3}\left(\mathrm{a}−\mathrm{b}\right)\mathrm{log2} \\ $$$$ \\ $$$$\:\:\:\mathrm{x}=\frac{\mathrm{2b}×\mathrm{log3}−\mathrm{3}\left(\mathrm{a}−\mathrm{b}\right)\mathrm{log2}}{\left(\mathrm{3}−\mathrm{a}\right)\mathrm{log2}−\left(\mathrm{a}−\mathrm{2}\right)\mathrm{log3}} \\ $$$$ \\ $$$$\:\:\:\:\mathrm{a}=\frac{\mathrm{log72}}{\mathrm{kog6}}=\:\frac{\mathrm{3log2}+\mathrm{2log3}}{\mathrm{log2}+\mathrm{log3}} \\ $$$$\:\:\:\mathrm{b}=\frac{\mathrm{log48}}{\mathrm{log6}}=\frac{\mathrm{4log2}+\mathrm{log3}}{\mathrm{log2}+\mathrm{log3}} \\ $$$$ \\ $$$$\:\left[\mathrm{a}−\mathrm{b}=\frac{\mathrm{log3}−\mathrm{log2}}{\mathrm{log2}+\mathrm{log3}}\right]\: \\ $$$$\mathrm{x}=\frac{\frac{\mathrm{2}\left(\mathrm{4log2}+\mathrm{log3}\right.}{\mathrm{log2}+\mathrm{log3}}\mathrm{log3}−\mathrm{3log2}\frac{\mathrm{log3}−\mathrm{log2}}{\mathrm{log2}+\mathrm{log3}}}{\mathrm{3}−\frac{\mathrm{3log2}+\mathrm{2log3}}{\mathrm{log2}+\mathrm{log3}}−\left(\frac{\left.\mathrm{3log2}+\mathrm{2log3}\right)}{\mathrm{log2}+\mathrm{log3}}−\mathrm{2}\right)\mathrm{log3}} \\ $$$$\:\:\:\:\mathrm{x}\:=\frac{\frac{\mathrm{8log2log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}−\mathrm{3log2}×\mathrm{log3}+\mathrm{3log}^{\mathrm{2}} \mathrm{2}}{\mathrm{log2}+\mathrm{log3}}}{\frac{\mathrm{3}\left(\mathrm{log2}+\mathrm{log3}\right)−\mathrm{3log2}−\mathrm{2log3}−\left[\mathrm{3log2log3}+\mathrm{2log}^{\mathrm{2}} \mathrm{3}−\mathrm{2log2log3}−\mathrm{2log}^{\mathrm{2}} \mathrm{3}\right]}{\mathrm{log2}+\mathrm{log3}}} \\ $$$$ \\ $$$$\:\:\mathrm{x}=\frac{\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}}{\mathrm{log3}\left(\mathrm{1}−\mathrm{log2}\right)} \\ $$$$ \\ $$$$ \\ $$$$\:\:\mathrm{y}=\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}=\frac{\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}}{\mathrm{log3}\left(\mathrm{1}−\mathrm{log2}\right)\frac{\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}}{\mathrm{1}}}×\left(\mathrm{3log2}+\mathrm{2log3}\right) \\ $$$$\mathrm{ax}=\frac{\mathrm{3log2}+\mathrm{2log3}}{\mathrm{log2}+\mathrm{log3}}×\frac{\left.\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right)}{\mathrm{log3}\left(\mathrm{1}−\mathrm{log2}\right)} \\ $$$$ \\ $$$$\:\:\mathrm{ax}=\:\:\:\frac{\left(\mathrm{3log2}+\mathrm{2log3}\right)×\left[\left(\mathrm{5log2}.\mathrm{log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}+\mathrm{3lo}^{\mathrm{2}} \mathrm{g2}\right)\right.}{\mathrm{log3}\left(\mathrm{1}−\mathrm{log2}\right)} \\ $$$$\:\:\:\mathrm{x}−\mathrm{b}=\frac{\mathrm{log3}\left(\mathrm{5kog2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}}{\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{log3}}−\frac{\mathrm{4log2}+\mathrm{log3}}{\mathrm{log2}+\mathrm{log3}}= \\ $$$$ \\ $$$$\:\:\:\:=\frac{\left(\mathrm{log2}+\mathrm{log3}\right)\left[\left(\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right]−\left[\left(\mathrm{4log2}+\mathrm{log3}\right)\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{log3}\right.\right.}{\left(\mathrm{1}−\mathrm{log2}\right)\left(\mathrm{log2}+\mathrm{log3}\right)\mathrm{log3}} \\ $$$$\:\:\:\:\frac{\mathrm{ax}}{\mathrm{x}−\mathrm{b}}=\:\frac{\left(\mathrm{3log2}+\mathrm{2log3}\right)\left[\left(\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right)\right.}{\left(\mathrm{1}−\mathrm{log2}\right)}×\frac{\left(\mathrm{1}−\mathrm{log2}\right)\left(\mathrm{log2}+\mathrm{log3}\right)\mathrm{log3}}{\left(\mathrm{log2}+\mathrm{log3}\right)\left[\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right]−\left[\left(\mathrm{4log2}+\mathrm{log3}\right)\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{log3}\right]}= \\ $$$$ \\ $$$$=\frac{\left[\left(\mathrm{3log2}+\mathrm{2log3}\right)\left(\mathrm{5log2log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}\right]+\left[\mathrm{3log}^{\mathrm{2}} \mathrm{2log3}\right)×\mathrm{log3}\left(\mathrm{1}−\mathrm{lkg2}\right)\left(\mathrm{log2}+\mathrm{log3}\right)\right]}{\left(\mathrm{1}−\mathrm{log2}\right)\left(\mathrm{log2}+\mathrm{lig3}\right)\left(\mathrm{5log2}.\mathrm{log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right)−\left[\mathrm{4log2}+\mathrm{log3}\right)\left(\mathrm{1}−\mathrm{log2}\right)\mathrm{log3}}= \\ $$$$ \\ $$$$=\frac{\left(\mathrm{3log2}+\mathrm{2log3}\right)\left(\mathrm{5log2log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}\right)+\left(\mathrm{3oig}^{\mathrm{2}} \mathrm{2log3}\right)\left(\mathrm{1}−\mathrm{log2}\right)\left(\mathrm{log2}+\mathrm{log3}\right)}{\left.\left(\left.\mathrm{1}−\mathrm{log2}\right)\left[\mathrm{log2}+\mathrm{log3}\right)\left(\mathrm{5log2log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right)−\left(\mathrm{4log2}+\mathrm{log3}\right)\mathrm{log3}\right)\right]} \\ $$$$ \\ $$$$\:\:\:\mathrm{y}=\frac{\left(\mathrm{3log2}+\mathrm{2log3}\right)\left[\mathrm{log3}\left(\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right]}{\left.\mathrm{log3}\left[\mathrm{5log2}+\mathrm{log3}\right)+\mathrm{3log}^{\mathrm{2}} \mathrm{2}\right)\left(\mathrm{log3}\left(\mathrm{1}−\mathrm{log2}\right)−\left(\mathrm{4log2log3}+\mathrm{log}^{\mathrm{2}} \mathrm{3}\right)\right.}\: \\ $$$$ \\ $$$$\:\:\mathrm{y}=\frac{\left[\mathrm{2log}^{\mathrm{3}} \mathrm{3}+\mathrm{9}.\mathrm{log}^{\mathrm{3}} \mathrm{2}+\left(\mathrm{log2}.\mathrm{log3}\right)\left(\mathrm{3}+\mathrm{21}.\mathrm{log}^{\mathrm{2}} \mathrm{2}+\:\mathrm{10}.\mathrm{log3}\right)\right]}{\left[\left(\mathrm{log}^{\mathrm{4}} \mathrm{3}+\mathrm{log}^{\mathrm{3}} \mathrm{3}−\mathrm{log2log3}\left(\mathrm{5log}^{\mathrm{2}} \mathrm{3}+\mathrm{5log3}+\mathrm{5}+\mathrm{22log2log3}\right)\right]\right.} \\ $$$$ \\ $$$$\:{de}\:{plus}\:\:\mathrm{x}=\mathrm{0}\:\:\:\:\:\mathrm{y}=\mathrm{0} \\ $$$${k} \\ $$
Answered by Frix last updated on 17/Oct/22
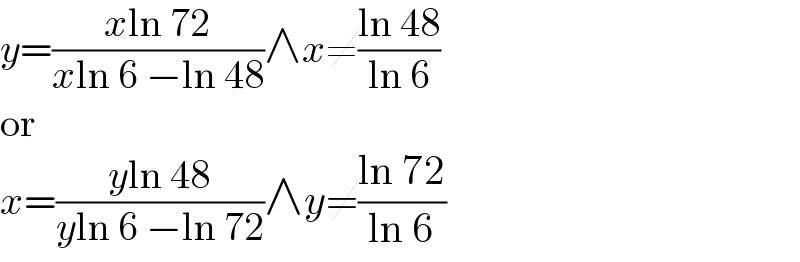
$${y}=\frac{{x}\mathrm{ln}\:\mathrm{72}}{{x}\mathrm{ln}\:\mathrm{6}\:−\mathrm{ln}\:\mathrm{48}}\wedge{x}\neq\frac{\mathrm{ln}\:\mathrm{48}}{\mathrm{ln}\:\mathrm{6}} \\ $$$$\mathrm{or} \\ $$$${x}=\frac{{y}\mathrm{ln}\:\mathrm{48}}{{y}\mathrm{ln}\:\mathrm{6}\:−\mathrm{ln}\:\mathrm{72}}\wedge{y}\neq\frac{\mathrm{ln}\:\mathrm{72}}{\mathrm{ln}\:\mathrm{6}} \\ $$
