
Question Number 178026 by aurpeyz last updated on 12/Oct/22

Commented by som(math1967) last updated on 12/Oct/22

$$\mathrm{46} \\ $$
Commented by aurpeyz last updated on 12/Oct/22

$${solution}\:{pls} \\ $$
Answered by FelipeLz last updated on 12/Oct/22
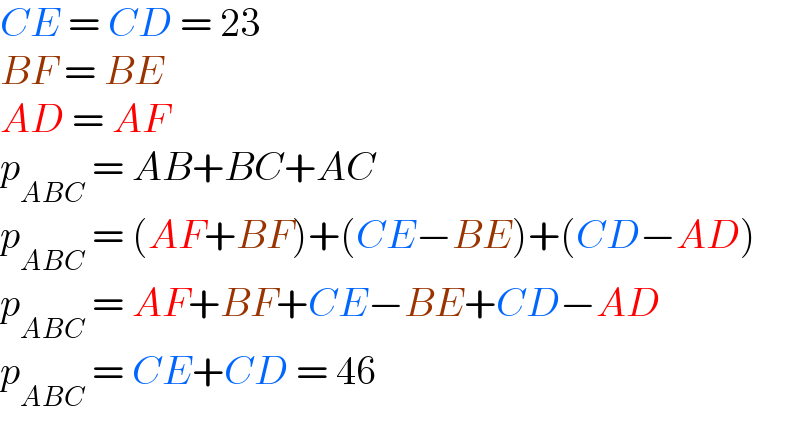
$${CE}\:=\:{CD}\:=\:\mathrm{23} \\ $$$${BF}\:=\:{BE} \\ $$$${AD}\:=\:{AF} \\ $$$${p}_{{ABC}} \:=\:{AB}+{BC}+{AC}\: \\ $$$${p}_{{ABC}} \:=\:\left({AF}+{BF}\right)+\left({CE}−{BE}\right)+\left({CD}−{AD}\right) \\ $$$${p}_{{ABC}} \:=\:{AF}+{BF}+{CE}−{BE}+{CD}−{AD} \\ $$$${p}_{{ABC}} \:=\:{CE}+{CD}\:=\:\mathrm{46} \\ $$
Commented by Tawa11 last updated on 12/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by aurpeyz last updated on 12/Oct/22

$${thanks} \\ $$
Commented by aurpeyz last updated on 12/Oct/22
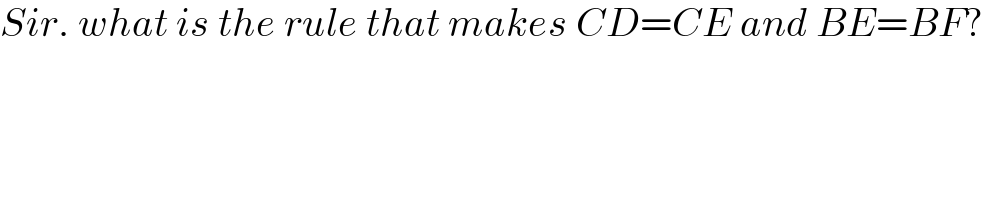
$${Sir}.\:{what}\:{is}\:{the}\:{rule}\:{that}\:{makes}\:{CD}={CE}\:{and}\:{BE}={BF}? \\ $$
Commented by aurpeyz last updated on 12/Oct/22

$${thanks}\:{so}\:{much} \\ $$
