
Question Number 177832 by HeferH last updated on 09/Oct/22
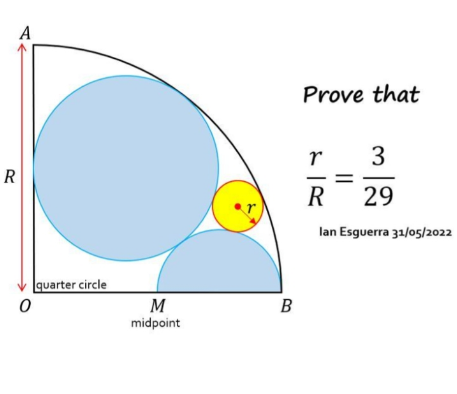
Answered by mr W last updated on 10/Oct/22
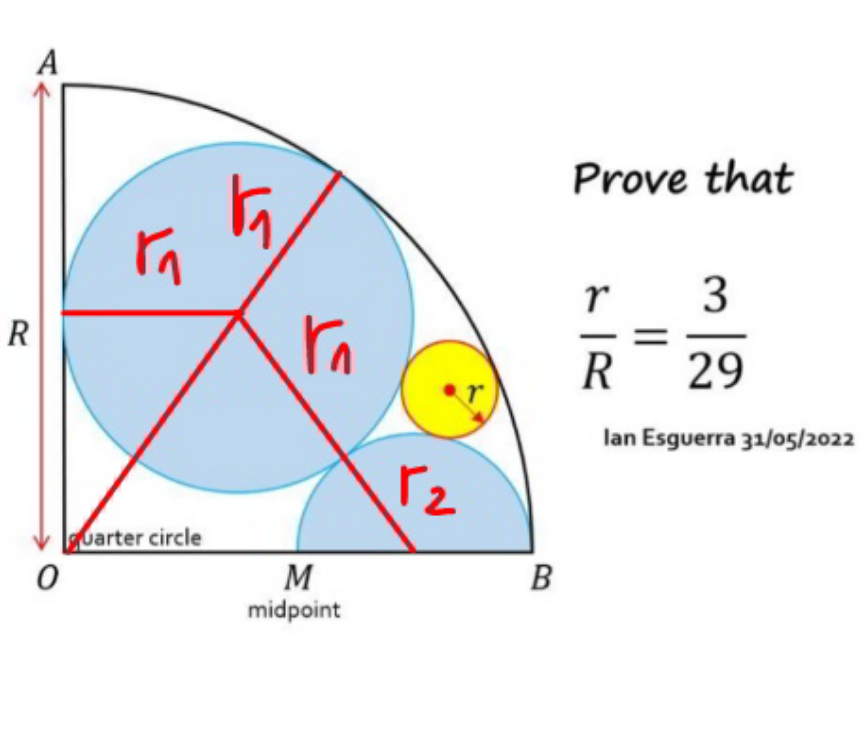
Commented by mr W last updated on 10/Oct/22
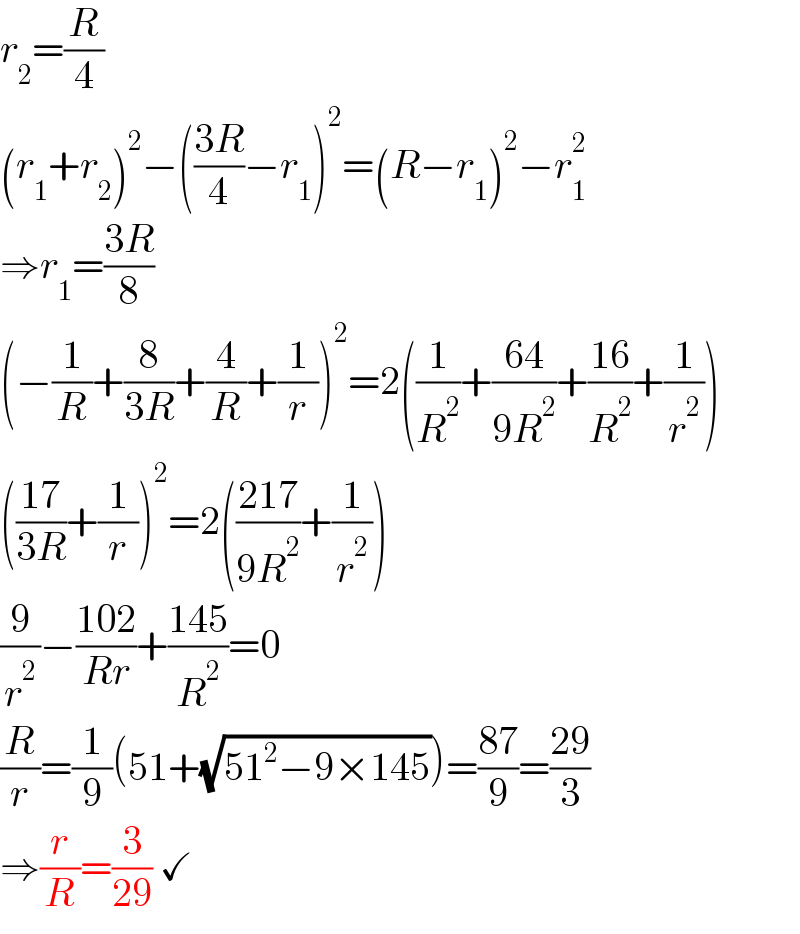
$${r}_{\mathrm{2}} =\frac{{R}}{\mathrm{4}} \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} −\left(\frac{\mathrm{3}{R}}{\mathrm{4}}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({R}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{\mathrm{3}{R}}{\mathrm{8}} \\ $$$$\left(−\frac{\mathrm{1}}{{R}}+\frac{\mathrm{8}}{\mathrm{3}{R}}+\frac{\mathrm{4}}{{R}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}^{\mathrm{2}} }+\frac{\mathrm{64}}{\mathrm{9}{R}^{\mathrm{2}} }+\frac{\mathrm{16}}{{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\left(\frac{\mathrm{17}}{\mathrm{3}{R}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{217}}{\mathrm{9}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{9}}{{r}^{\mathrm{2}} }−\frac{\mathrm{102}}{{Rr}}+\frac{\mathrm{145}}{{R}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}}{\mathrm{9}}\left(\mathrm{51}+\sqrt{\mathrm{51}^{\mathrm{2}} −\mathrm{9}×\mathrm{145}}\right)=\frac{\mathrm{87}}{\mathrm{9}}=\frac{\mathrm{29}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\mathrm{3}}{\mathrm{29}}\:\checkmark \\ $$
Commented by Tawa11 last updated on 10/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
