Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 177796 by mr W last updated on 09/Oct/22

Commented by mr W last updated on 09/Oct/22

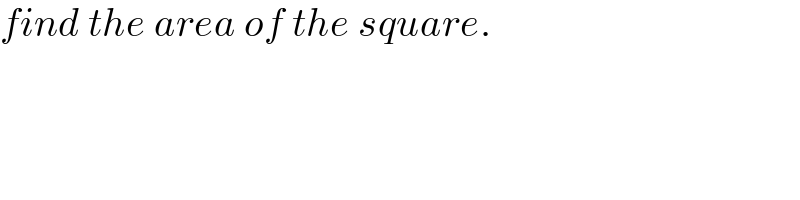
find the area of the square.

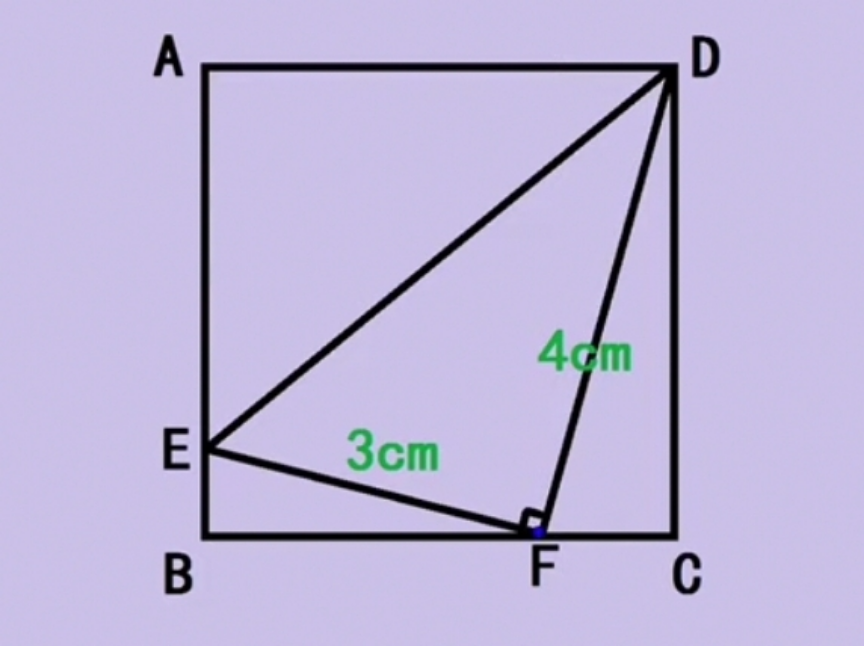
$${find}\:{the}\:{area}\:{of}\:{the}\:{square}. \\ $$

Commented by mr W last updated on 09/Oct/22

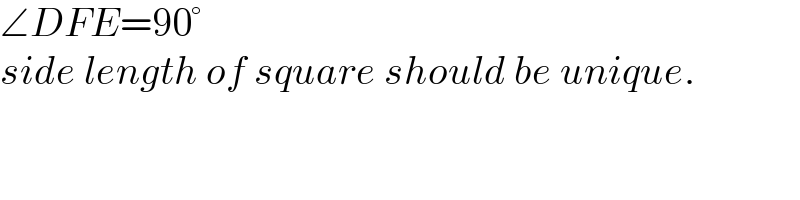
∠DFE=90° side length of square should be unique.

$$\angle{DFE}=\mathrm{90}° \\ $$$${side}\:{length}\:{of}\:{square}\:{should}\:{be}\:{unique}. \\ $$

Commented by Rasheed.Sindhi last updated on 09/Oct/22

You′re right sir!

$${You}'{re}\:{right}\:\boldsymbol{{sir}}! \\ $$

Commented by Rasheed.Sindhi last updated on 09/Oct/22

Sir I think that the area depends upon BE or FC. In other words the area of square is not unique.

$$\boldsymbol{{Sir}}\:{I}\:{think}\:{that}\:{the}\:{area}\:{depends}\: \\ $$$${upon}\:{BE}\:{or}\:{FC}.\:{In}\:{other}\:{words} \\ $$$${the}\:{area}\:{of}\:{square}\:{is}\:{not}\:{unique}. \\ $$

Answered by mr W last updated on 09/Oct/22

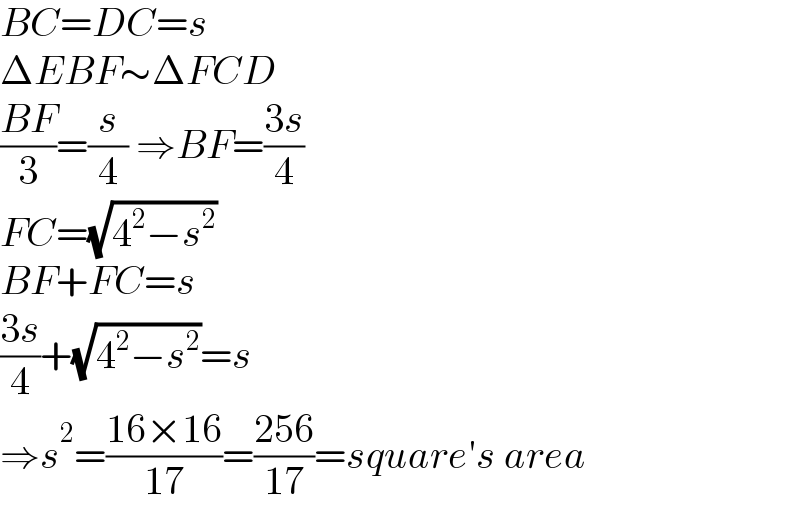
BC=DC=s ΔEBF∼ΔFCD ((BF)/3)=(s/4) ⇒BF=((3s)/4) FC=(√(4^2 −s^2 )) BF+FC=s ((3s)/4)+(√(4^2 −s^2 ))=s ⇒s^2 =((16×16)/(17))=((256)/(17))=square′s area

$${BC}={DC}={s} \\ $$$$\Delta{EBF}\sim\Delta{FCD} \\ $$$$\frac{{BF}}{\mathrm{3}}=\frac{{s}}{\mathrm{4}}\:\Rightarrow{BF}=\frac{\mathrm{3}{s}}{\mathrm{4}} \\ $$$${FC}=\sqrt{\mathrm{4}^{\mathrm{2}} −{s}^{\mathrm{2}} } \\ $$$${BF}+{FC}={s} \\ $$$$\frac{\mathrm{3}{s}}{\mathrm{4}}+\sqrt{\mathrm{4}^{\mathrm{2}} −{s}^{\mathrm{2}} }={s} \\ $$$$\Rightarrow{s}^{\mathrm{2}} =\frac{\mathrm{16}×\mathrm{16}}{\mathrm{17}}=\frac{\mathrm{256}}{\mathrm{17}}={square}'{s}\:{area} \\ $$

Commented by Tawa11 last updated on 09/Oct/22

Great sirs

$$\mathrm{Great}\:\mathrm{sirs} \\ $$

Answered by cortano1 last updated on 09/Oct/22

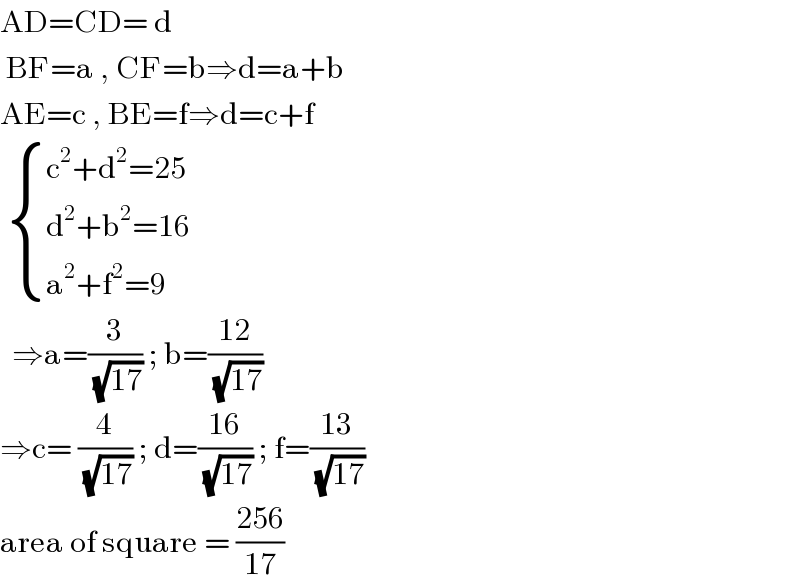
AD=CD= d BF=a , CF=b⇒d=a+b AE=c , BE=f⇒d=c+f { ((c^2 +d^2 =25)),((d^2 +b^2 =16)),((a^2 +f^2 =9)) :} ⇒a=(3/( (√(17)))) ; b=((12)/( (√(17)))) ⇒c= (4/( (√(17)))) ; d=((16)/( (√(17)))) ; f=((13)/( (√(17)))) area of square = ((256)/(17))

$$\mathrm{AD}=\mathrm{CD}=\:\mathrm{d} \\ $$$$\:\mathrm{BF}=\mathrm{a}\:,\:\mathrm{CF}=\mathrm{b}\Rightarrow\mathrm{d}=\mathrm{a}+\mathrm{b} \\ $$$$\mathrm{AE}=\mathrm{c}\:,\:\mathrm{BE}=\mathrm{f}\Rightarrow\mathrm{d}=\mathrm{c}+\mathrm{f} \\ $$$$\:\begin{cases}{\mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} =\mathrm{25}}\\{\mathrm{d}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{16}}\\{\mathrm{a}^{\mathrm{2}} +\mathrm{f}^{\mathrm{2}} =\mathrm{9}}\end{cases} \\ $$$$\:\:\Rightarrow\mathrm{a}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{17}}}\:;\:\mathrm{b}=\frac{\mathrm{12}}{\:\sqrt{\mathrm{17}}} \\ $$$$\Rightarrow\mathrm{c}=\:\frac{\mathrm{4}}{\:\sqrt{\mathrm{17}}}\:;\:\mathrm{d}=\frac{\mathrm{16}}{\:\sqrt{\mathrm{17}}}\:;\:\mathrm{f}=\frac{\mathrm{13}}{\:\sqrt{\mathrm{17}}} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{square}\:=\:\frac{\mathrm{256}}{\mathrm{17}} \\ $$

Answered by cortano1 last updated on 09/Oct/22

((256)/(17)) ?

$$\frac{\mathrm{256}}{\mathrm{17}}\:? \\ $$

Commented by mr W last updated on 09/Oct/22

yes!

$${yes}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com