
Question Number 17743 by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17

Answered by mrW1 last updated on 10/Jul/17
![let k=((√2)/2) l A(0,k,0) B(k,0,0) C(0,−k,0) D(−k,0,0) M(p,q,r) ⇒a^2 =p^2 +(q−k)^2 +r^2 ...(i) ⇒b^2 =(p−k)^2 +q^2 +r^2 ...(ii) ⇒c^2 =p^2 +(q+k)^2 +r^2 ...(iii) ⇒d^2 =(p+k)^2 +q^2 +r^2 ...(iv) a^2 +c^2 =2p^2 +2q^2 +2r^2 +2k^2 =2(p^2 +q^2 +r^2 +k^2 ) b^2 +d^2 =2p^2 +2q^2 +2r^2 +2k^2 =2(p^2 +q^2 +r^2 +k^2 ) ⇒a^2 +c^2 =b^2 +d^2 (iii)−(i): c^2 −a^2 =4qk ⇒q=((c^2 −a^2 )/(4k)) (iv)−(ii): d^2 −b^2 =4pk ⇒p=((d^2 −b^2 )/(4k)) from (i): r^2 =−[p^2 +(q−k)^2 −a^2 ] =−[(((d^2 −b^2 )^2 )/(16k^2 ))+(((c^2 −a^2 )/(4k))−k)^2 −a^2 ] =−[(((d^2 −b^2 )^2 +(c^2 −a^2 −4k^2 )^2 −16a^2 k^2 )/(16k^2 ))] =−[((d^4 +b^4 −2d^2 b^2 +c^4 +a^4 +16k^4 −2a^2 c^2 −8k^2 c^2 +8k^2 a^2 −16a^2 k^2 )/(16k^2 ))] =−[((a^4 +b^4 +c^4 +d^4 −2(a^2 c^2 +d^2 b^2 )+16k^4 −8k^2 (a^2 +c^2 ))/(16k^2 ))] =−[(((a^2 −c^2 )^2 +(b^2 −d^2 )^2 −8k^2 (a^2 +c^2 )+16k^4 )/(16k^2 ))] =−[(((a^2 −c^2 )^2 +(b^2 −d^2 )^2 −8k^2 (a^2 +c^2 −2k^2 ))/(16k^2 ))] =−[(((a^2 −c^2 )^2 +(b^2 −d^2 )^2 −4 l^2 (a^2 +c^2 −l^2 ))/(8 l^2 ))] ⇒h=∣r∣=((√(4 l^2 (a^2 +c^2 −l^2 )−(a^2 −c^2 )^2 −(b^2 −d^2 )^2 ))/(2(√2) l))](Q17753.png)
$$\mathrm{let}\:\mathrm{k}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\mathrm{l} \\ $$$$\mathrm{A}\left(\mathrm{0},\mathrm{k},\mathrm{0}\right) \\ $$$$\mathrm{B}\left(\mathrm{k},\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{C}\left(\mathrm{0},−\mathrm{k},\mathrm{0}\right) \\ $$$$\mathrm{D}\left(−\mathrm{k},\mathrm{0},\mathrm{0}\right) \\ $$$$\mathrm{M}\left(\mathrm{p},\mathrm{q},\mathrm{r}\right) \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\left(\mathrm{q}−\mathrm{k}\right)^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \:\:\:...\left(\mathrm{i}\right) \\ $$$$\Rightarrow\mathrm{b}^{\mathrm{2}} =\left(\mathrm{p}−\mathrm{k}\right)^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \:\:\:...\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{c}^{\mathrm{2}} =\mathrm{p}^{\mathrm{2}} +\left(\mathrm{q}+\mathrm{k}\right)^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \:\:\:...\left(\mathrm{iii}\right) \\ $$$$\Rightarrow\mathrm{d}^{\mathrm{2}} =\left(\mathrm{p}+\mathrm{k}\right)^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} \:\:\:...\left(\mathrm{iv}\right) \\ $$$$ \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{2p}^{\mathrm{2}} +\mathrm{2q}^{\mathrm{2}} +\mathrm{2r}^{\mathrm{2}} +\mathrm{2k}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right) \\ $$$$\mathrm{b}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} =\mathrm{2p}^{\mathrm{2}} +\mathrm{2q}^{\mathrm{2}} +\mathrm{2r}^{\mathrm{2}} +\mathrm{2k}^{\mathrm{2}} =\mathrm{2}\left(\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} \\ $$$$ \\ $$$$\left(\mathrm{iii}\right)−\left(\mathrm{i}\right): \\ $$$$\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} =\mathrm{4qk} \\ $$$$\Rightarrow\mathrm{q}=\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{4k}} \\ $$$$\left(\mathrm{iv}\right)−\left(\mathrm{ii}\right): \\ $$$$\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\mathrm{4pk} \\ $$$$\Rightarrow\mathrm{p}=\frac{\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }{\mathrm{4k}} \\ $$$$ \\ $$$$\mathrm{from}\:\left(\mathrm{i}\right): \\ $$$$\mathrm{r}^{\mathrm{2}} =−\left[\mathrm{p}^{\mathrm{2}} +\left(\mathrm{q}−\mathrm{k}\right)^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right] \\ $$$$=−\left[\frac{\left(\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16k}^{\mathrm{2}} }+\left(\frac{\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{4k}}−\mathrm{k}\right)^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right] \\ $$$$=−\left[\frac{\left(\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} −\mathrm{4k}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{16a}^{\mathrm{2}} \mathrm{k}^{\mathrm{2}} }{\mathrm{16k}^{\mathrm{2}} }\right] \\ $$$$=−\left[\frac{\mathrm{d}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} −\mathrm{2d}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{4}} +\mathrm{a}^{\mathrm{4}} +\mathrm{16k}^{\mathrm{4}} −\mathrm{2a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{8k}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{8k}^{\mathrm{2}} \mathrm{a}^{\mathrm{2}} −\mathrm{16a}^{\mathrm{2}} \mathrm{k}^{\mathrm{2}} }{\mathrm{16k}^{\mathrm{2}} }\right] \\ $$$$=−\left[\frac{\mathrm{a}^{\mathrm{4}} +\mathrm{b}^{\mathrm{4}} +\mathrm{c}^{\mathrm{4}} +\mathrm{d}^{\mathrm{4}} −\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \right)+\mathrm{16k}^{\mathrm{4}} −\mathrm{8k}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)}{\mathrm{16k}^{\mathrm{2}} }\right] \\ $$$$=−\left[\frac{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}^{\mathrm{2}} −\mathrm{d}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{8k}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{16k}^{\mathrm{4}} }{\mathrm{16k}^{\mathrm{2}} }\right] \\ $$$$=−\left[\frac{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}^{\mathrm{2}} −\mathrm{d}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{8k}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{2k}^{\mathrm{2}} \right)}{\mathrm{16k}^{\mathrm{2}} }\right] \\ $$$$=−\left[\frac{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{b}^{\mathrm{2}} −\mathrm{d}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\:\mathrm{l}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{l}^{\mathrm{2}} \right)}{\mathrm{8}\:\mathrm{l}^{\mathrm{2}} }\right] \\ $$$$\Rightarrow\mathrm{h}=\mid\mathrm{r}\mid=\frac{\sqrt{\mathrm{4}\:\mathrm{l}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{l}^{\mathrm{2}} \right)−\left(\mathrm{a}^{\mathrm{2}} −\mathrm{c}^{\mathrm{2}} \right)^{\mathrm{2}} −\left(\mathrm{b}^{\mathrm{2}} −\mathrm{d}^{\mathrm{2}} \right)^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{l}} \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17
$${thank}\:{you}\:{dear}\:{mrW}\mathrm{1}. \\ $$$${first}\:{and}\:{always}\:{the}\:{best}. \\ $$
Answered by ajfour last updated on 10/Jul/17

Commented by ajfour last updated on 10/Jul/17
![AP^2 =a^2 =h^2 +(x−k)^2 +y^2 BP^2 =b^2 =h^2 +x^2 +(y−k)^2 CP^2 =c^2 =h^2 +(x+k)^2 +y^2 DP^2 =d^2 =h^2 +x^2 +(y+k)^2 a^2 +c^2 =b^2 +d^2 =2(h^2 +x^2 +y^2 +k^2 ) .....(i) c^2 −a^2 =4kx ; d^2 −b^2 =4ky ⇒16k^2 (x^2 +y^2 )=(c^2 −a^2 )^2 +(d^2 −b^2 )^2 a^2 +b^2 +c^2 +d^2 = 4(h^2 +x^2 +y^2 +k^2 ) so, 16k^2 h^2 =4k^2 (a^2 +b^2 +c^2 +d^2 ) −16k^2 (x^2 +y^2 +k^2 ) 16k^2 h^2 =4k^2 (a^2 +b^2 +c^2 +d^2 ) −[(c^2 −a^2 )^2 +(d^2 −b^2 )^2 ]−16k^4 h=(√(((a^2 +b^2 +c^2 +d^2 )/4)−(((c^2 −a^2 )+(d^2 −b^2 )^2 )/(16k^2 ))−k^2 )) with 2k^2 =l^2 .](Q17762.png)
$$\mathrm{AP}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} +\left(\mathrm{x}−\mathrm{k}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{BP}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{k}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{CP}^{\mathrm{2}} =\mathrm{c}^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} +\left(\mathrm{x}+\mathrm{k}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{DP}^{\mathrm{2}} =\mathrm{d}^{\mathrm{2}} =\mathrm{h}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\left(\mathrm{y}+\mathrm{k}\right)^{\mathrm{2}} \\ $$$$\:\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} \:=\mathrm{2}\left(\mathrm{h}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\left(\mathrm{i}\right) \\ $$$$\:\:\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} =\mathrm{4kx}\:\:;\:\:\:\:\:\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} =\mathrm{4ky} \\ $$$$\Rightarrow\mathrm{16k}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)=\left(\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} =\:\mathrm{4}\left(\mathrm{h}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right) \\ $$$$\mathrm{so},\:\:\mathrm{16k}^{\mathrm{2}} \mathrm{h}^{\mathrm{2}} =\mathrm{4k}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{16k}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{k}^{\mathrm{2}} \right) \\ $$$$\:\mathrm{16k}^{\mathrm{2}} \mathrm{h}^{\mathrm{2}} =\mathrm{4k}^{\mathrm{2}} \left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:−\left[\left(\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{2}} +\left(\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} \right]−\mathrm{16k}^{\mathrm{4}} \\ $$$$\mathrm{h}=\sqrt{\frac{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} }{\mathrm{4}}−\frac{\left(\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} \right)+\left(\mathrm{d}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{16k}^{\mathrm{2}} }−\mathrm{k}^{\mathrm{2}} }\: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{with}\:\:\:\mathrm{2k}^{\mathrm{2}} ={l}^{\mathrm{2}} \:. \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17

$${thank}\:{you}\:{dear}\:{mr}\:{Ajfour}. \\ $$$${your}\:{answers}\:{are}\:{spicial}\:{and}\:{different} \\ $$$${any}\:{time}. \\ $$
Commented by ajfour last updated on 10/Jul/17

$$\mathrm{but}\:\mathrm{mrW1}\:\mathrm{Sir}'\mathrm{s}\:\mathrm{answer}\:\mathrm{dont}\:\mathrm{agree} \\ $$$$\mathrm{with}\:\mathrm{my}\:\mathrm{answer}.\mathrm{please}\:\mathrm{find}\:\mathrm{the}\:\mathrm{error}. \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17
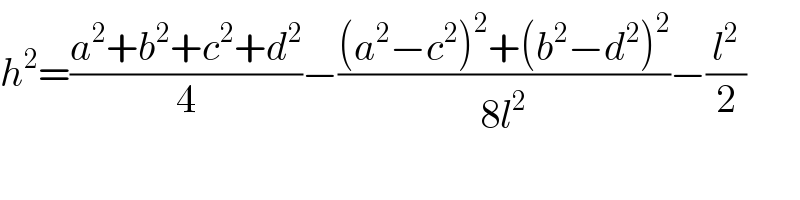
$${h}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} }{\mathrm{4}}−\frac{\left({a}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{d}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{8}{l}^{\mathrm{2}} }−\frac{{l}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by mrW1 last updated on 10/Jul/17

$$\mathrm{I}\:\mathrm{had}\:\mathrm{a}\:\mathrm{mistake}\:\mathrm{with}\:``−''\mathrm{sign}.\:\mathrm{But} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{even}\:\mathrm{when}\:\mathrm{we} \\ $$$$\mathrm{used}\:\mathrm{different}\:\mathrm{expressions},\:\mathrm{since} \\ $$$$\mathrm{a}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} +\mathrm{d}^{\mathrm{2}} . \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 10/Jul/17
$${thanks}\:{for}\:{your}\:{care}\:{and}\:{correction}. \\ $$
