Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 176906 by HeferH last updated on 27/Sep/22

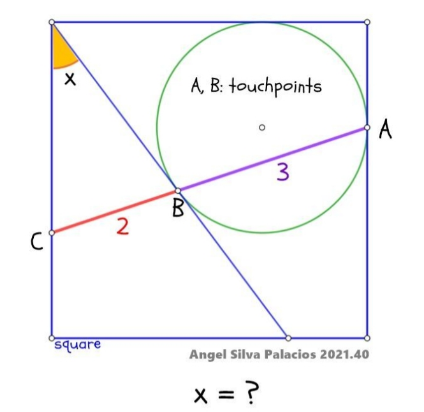
Commented by ajfour last updated on 27/Sep/22

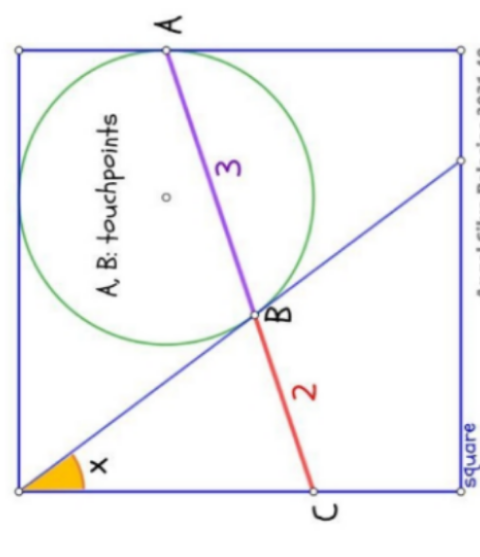
Commented by ajfour last updated on 27/Sep/22

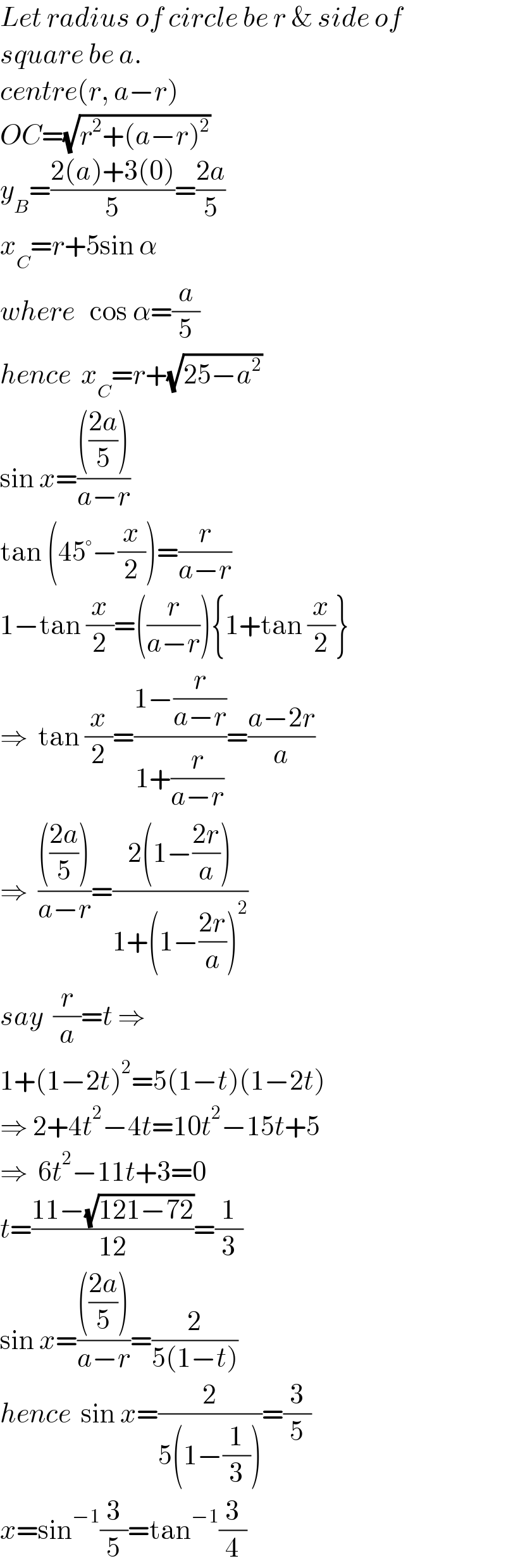
Let radius of circle be r & side of square be a. centre(r, a−r) OC=(√(r^2 +(a−r)^2 )) y_B =((2(a)+3(0))/5)=((2a)/5) x_C =r+5sin α where cos α=(a/5) hence x_C =r+(√(25−a^2 )) sin x=(((((2a)/5)))/(a−r)) tan (45°−(x/2))=(r/(a−r)) 1−tan (x/2)=((r/(a−r))){1+tan (x/2)} ⇒ tan (x/2)=((1−(r/(a−r)))/(1+(r/(a−r))))=((a−2r)/a) ⇒ (((((2a)/5)))/(a−r))=((2(1−((2r)/a)))/(1+(1−((2r)/a))^2 )) say (r/a)=t ⇒ 1+(1−2t)^2 =5(1−t)(1−2t) ⇒ 2+4t^2 −4t=10t^2 −15t+5 ⇒ 6t^2 −11t+3=0 t=((11−(√(121−72)))/(12))=(1/3) sin x=(((((2a)/5)))/(a−r))=(2/(5(1−t))) hence sin x=(2/(5(1−(1/3))))=(3/5) x=sin^(−1) (3/5)=tan^(−1) (3/4)

$${Let}\:{radius}\:{of}\:{circle}\:{be}\:{r}\:\&\:{side}\:{of} \\ $$$${square}\:{be}\:{a}. \\ $$$${centre}\left({r},\:{a}−{r}\right) \\ $$$${OC}=\sqrt{{r}^{\mathrm{2}} +\left({a}−{r}\right)^{\mathrm{2}} } \\ $$$${y}_{{B}} =\frac{\mathrm{2}\left({a}\right)+\mathrm{3}\left(\mathrm{0}\right)}{\mathrm{5}}=\frac{\mathrm{2}{a}}{\mathrm{5}} \\ $$$${x}_{{C}} ={r}+\mathrm{5sin}\:\alpha \\ $$$${where}\:\:\:\mathrm{cos}\:\alpha=\frac{{a}}{\mathrm{5}} \\ $$$${hence}\:\:{x}_{{C}} ={r}+\sqrt{\mathrm{25}−{a}^{\mathrm{2}} } \\ $$$$\mathrm{sin}\:{x}=\frac{\left(\frac{\mathrm{2}{a}}{\mathrm{5}}\right)}{{a}−{r}} \\ $$$$\mathrm{tan}\:\left(\mathrm{45}°−\frac{{x}}{\mathrm{2}}\right)=\frac{{r}}{{a}−{r}} \\ $$$$\mathrm{1}−\mathrm{tan}\:\frac{{x}}{\mathrm{2}}=\left(\frac{{r}}{{a}−{r}}\right)\left\{\mathrm{1}+\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\right\} \\ $$$$\Rightarrow\:\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}=\frac{\mathrm{1}−\frac{{r}}{{a}−{r}}}{\mathrm{1}+\frac{{r}}{{a}−{r}}}=\frac{{a}−\mathrm{2}{r}}{{a}} \\ $$$$\Rightarrow\:\:\frac{\left(\frac{\mathrm{2}{a}}{\mathrm{5}}\right)}{{a}−{r}}=\frac{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{2}{r}}{{a}}\right)}{\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{2}{r}}{{a}}\right)^{\mathrm{2}} } \\ $$$${say}\:\:\frac{{r}}{{a}}={t}\:\Rightarrow \\ $$$$\mathrm{1}+\left(\mathrm{1}−\mathrm{2}{t}\right)^{\mathrm{2}} =\mathrm{5}\left(\mathrm{1}−{t}\right)\left(\mathrm{1}−\mathrm{2}{t}\right) \\ $$$$\Rightarrow\:\mathrm{2}+\mathrm{4}{t}^{\mathrm{2}} −\mathrm{4}{t}=\mathrm{10}{t}^{\mathrm{2}} −\mathrm{15}{t}+\mathrm{5} \\ $$$$\Rightarrow\:\:\mathrm{6}{t}^{\mathrm{2}} −\mathrm{11}{t}+\mathrm{3}=\mathrm{0} \\ $$$${t}=\frac{\mathrm{11}−\sqrt{\mathrm{121}−\mathrm{72}}}{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{sin}\:{x}=\frac{\left(\frac{\mathrm{2}{a}}{\mathrm{5}}\right)}{{a}−{r}}=\frac{\mathrm{2}}{\mathrm{5}\left(\mathrm{1}−{t}\right)} \\ $$$${hence}\:\:\mathrm{sin}\:{x}=\frac{\mathrm{2}}{\mathrm{5}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right)}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${x}=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{5}}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}} \\ $$

Commented by Tawa11 last updated on 28/Sep/22

Great sir.

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Answered by mr W last updated on 27/Sep/22

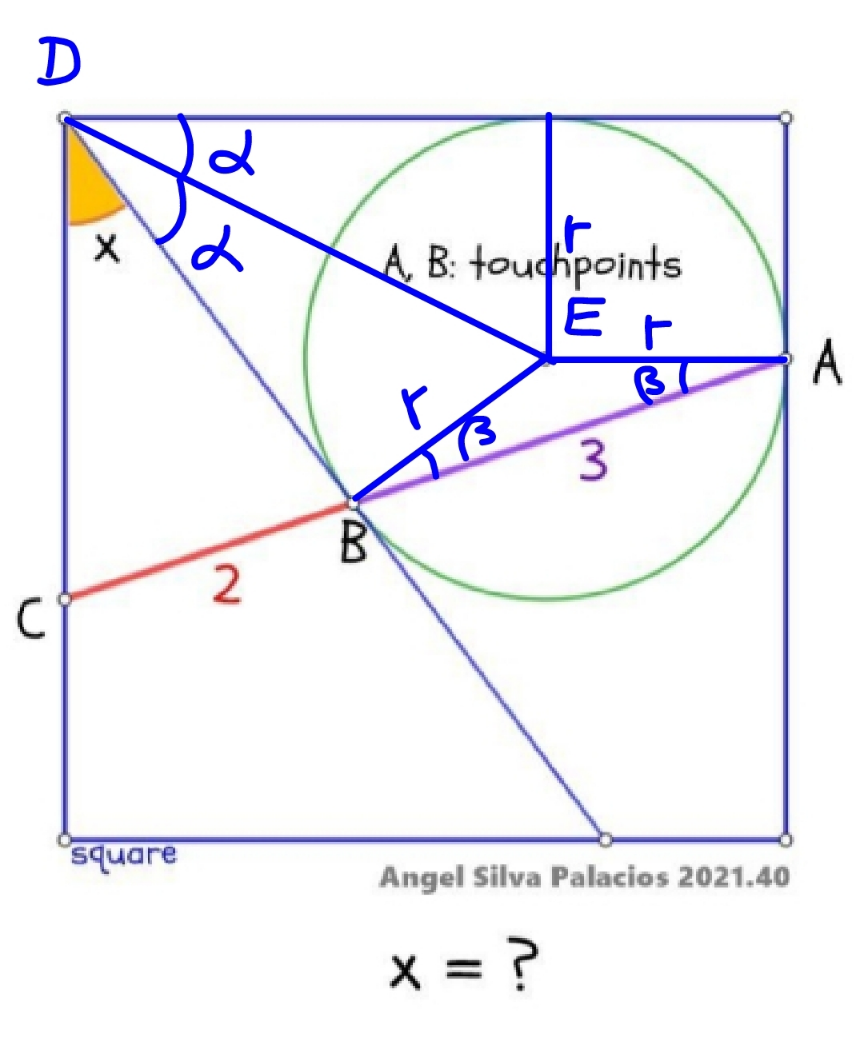
Commented by mr W last updated on 27/Sep/22

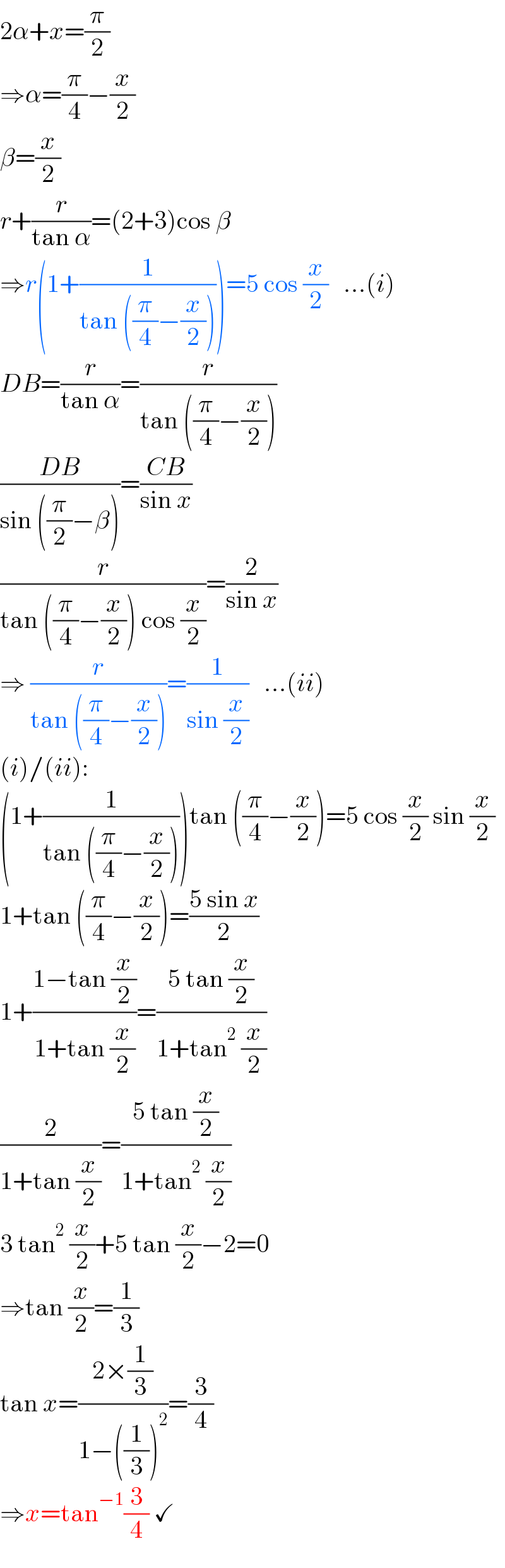
2α+x=(π/2) ⇒α=(π/4)−(x/2) β=(x/2) r+(r/(tan α))=(2+3)cos β ⇒r(1+(1/(tan ((π/4)−(x/2)))))=5 cos (x/2) ...(i) DB=(r/(tan α))=(r/(tan ((π/4)−(x/2)))) ((DB)/(sin ((π/2)−β)))=((CB)/(sin x)) (r/(tan ((π/4)−(x/2)) cos (x/2)))=(2/(sin x)) ⇒ (r/(tan ((π/4)−(x/2))))=(1/(sin (x/2))) ...(ii) (i)/(ii): (1+(1/(tan ((π/4)−(x/2)))))tan ((π/4)−(x/2))=5 cos (x/2) sin (x/2) 1+tan ((π/4)−(x/2))=((5 sin x)/2) 1+((1−tan (x/2))/(1+tan (x/2)))=((5 tan (x/2))/(1+tan^2 (x/2))) (2/(1+tan (x/2)))=((5 tan (x/2))/(1+tan^2 (x/2))) 3 tan^2 (x/2)+5 tan (x/2)−2=0 ⇒tan (x/2)=(1/3) tan x=((2×(1/3))/(1−((1/3))^2 ))=(3/4) ⇒x=tan^(−1) (3/4) ✓

$$\mathrm{2}\alpha+{x}=\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\alpha=\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}} \\ $$$$\beta=\frac{{x}}{\mathrm{2}} \\ $$$${r}+\frac{{r}}{\mathrm{tan}\:\alpha}=\left(\mathrm{2}+\mathrm{3}\right)\mathrm{cos}\:\beta \\ $$$$\Rightarrow{r}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}\right)=\mathrm{5}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:\:\:...\left({i}\right) \\ $$$${DB}=\frac{{r}}{\mathrm{tan}\:\alpha}=\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)} \\ $$$$\frac{{DB}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\beta\right)}=\frac{{CB}}{\mathrm{sin}\:{x}} \\ $$$$\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}=\frac{\mathrm{2}}{\mathrm{sin}\:{x}} \\ $$$$\Rightarrow\:\frac{{r}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{sin}\:\frac{{x}}{\mathrm{2}}}\:\:\:...\left({ii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}\right)\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)=\mathrm{5}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)=\frac{\mathrm{5}\:\mathrm{sin}\:{x}}{\mathrm{2}} \\ $$$$\mathrm{1}+\frac{\mathrm{1}−\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}=\frac{\mathrm{5}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}=\frac{\mathrm{5}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}} \\ $$$$\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+\mathrm{5}\:\mathrm{tan}\:\frac{{x}}{\mathrm{2}}−\mathrm{2}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\frac{{x}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{3}}{\mathrm{4}}\:\checkmark \\ $$

Commented by Tawa11 last updated on 28/Sep/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com