
Question Number 176776 by cherokeesay last updated on 26/Sep/22
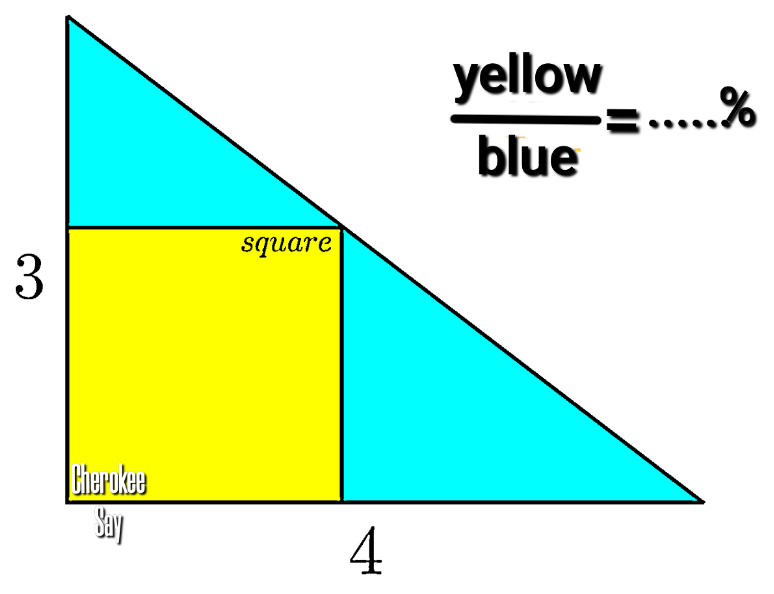
Answered by BaliramKumar last updated on 27/Sep/22
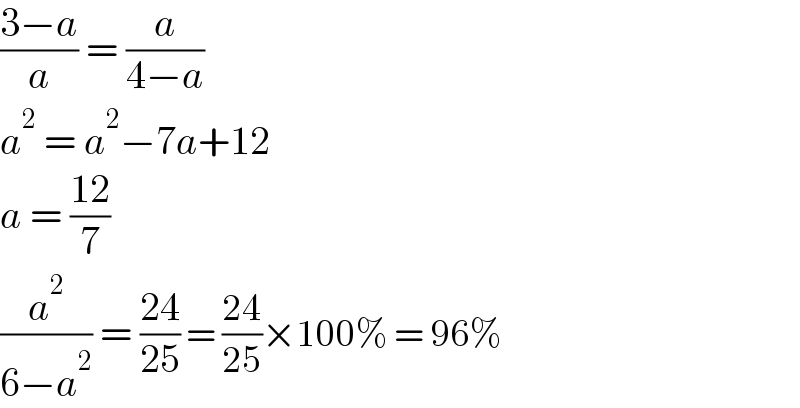
$$\frac{\mathrm{3}−{a}}{{a}}\:=\:\frac{{a}}{\mathrm{4}−{a}} \\ $$$${a}^{\mathrm{2}} \:=\:{a}^{\mathrm{2}} −\mathrm{7}{a}+\mathrm{12} \\ $$$${a}\:=\:\frac{\mathrm{12}}{\mathrm{7}} \\ $$$$\frac{{a}^{\mathrm{2}} }{\mathrm{6}−{a}^{\mathrm{2}} }\:=\:\frac{\mathrm{24}}{\mathrm{25}}\:=\:\frac{\mathrm{24}}{\mathrm{25}}×\mathrm{100\%}\:=\:\mathrm{96\%} \\ $$
Commented by cherokeesay last updated on 26/Sep/22

$${Nice}\:!\:{thank}\:{you}\:! \\ $$
Answered by a.lgnaoui last updated on 26/Sep/22
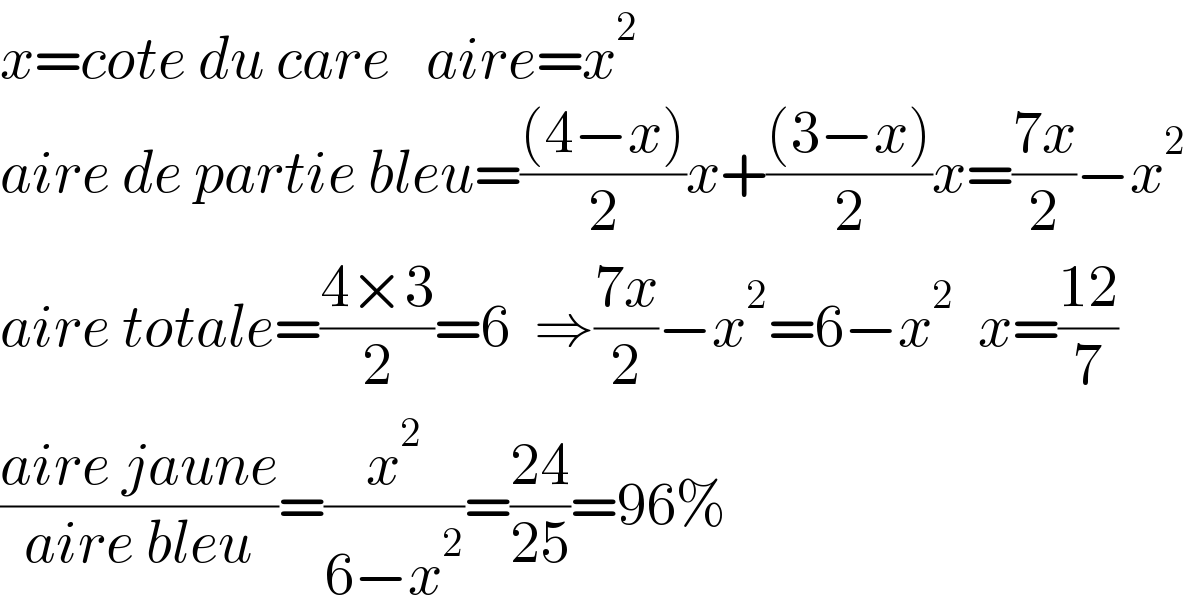
$${x}={cote}\:{du}\:{care}\:\:\:{aire}={x}^{\mathrm{2}} \\ $$$${aire}\:{de}\:{partie}\:{bleu}=\frac{\left(\mathrm{4}−{x}\right)}{\mathrm{2}}{x}+\frac{\left(\mathrm{3}−{x}\right)}{\mathrm{2}}{x}=\frac{\mathrm{7}{x}}{\mathrm{2}}−{x}^{\mathrm{2}} \\ $$$${aire}\:{totale}=\frac{\mathrm{4}×\mathrm{3}}{\mathrm{2}}=\mathrm{6}\:\:\Rightarrow\frac{\mathrm{7}{x}}{\mathrm{2}}−{x}^{\mathrm{2}} =\mathrm{6}−{x}^{\mathrm{2}} \:\:{x}=\frac{\mathrm{12}}{\mathrm{7}} \\ $$$$\frac{{aire}\:{jaune}}{{aire}\:{bleu}}=\frac{{x}^{\mathrm{2}} }{\mathrm{6}−{x}^{\mathrm{2}} }=\frac{\mathrm{24}}{\mathrm{25}}=\mathrm{96\%} \\ $$
Commented by cherokeesay last updated on 26/Sep/22

$${Great}\:!\:{thank}\:{you} \\ $$
