Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 176710 by eka last updated on 25/Sep/22

Answered by a.lgnaoui last updated on 26/Sep/22

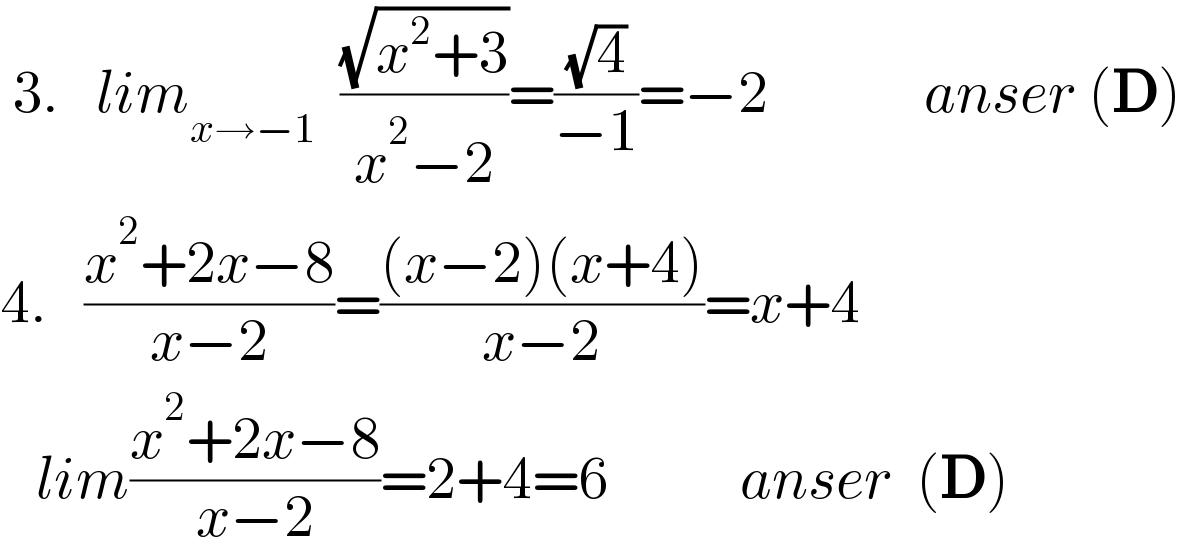
3. lim_(x→−1) ((√(x^2 +3))/(x^2 −2))=((√4)/(−1))=−2 anser (D) 4. ((x^2 +2x−8)/(x−2))=(((x−2)(x+4))/(x−2))=x+4 lim((x^2 +2x−8)/(x−2))=2+4=6 anser (D)

$$\:\mathrm{3}.\:\:\:{lim}_{{x}\rightarrow−\mathrm{1}} \:\:\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{2}}=\frac{\sqrt{\mathrm{4}}}{−\mathrm{1}}=−\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:{anser}\:\left(\boldsymbol{\mathrm{D}}\right) \\ $$$$\mathrm{4}.\:\:\:\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{8}}{{x}−\mathrm{2}}=\frac{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{4}\right)}{{x}−\mathrm{2}}={x}+\mathrm{4} \\ $$$$\:\:\:{lim}\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{8}}{{x}−\mathrm{2}}=\mathrm{2}+\mathrm{4}=\mathrm{6}\:\:\:\:\:\:\:\:\:\:\:{anser}\:\:\left(\boldsymbol{\mathrm{D}}\right) \\ $$

Answered by Rasheed.Sindhi last updated on 25/Sep/22

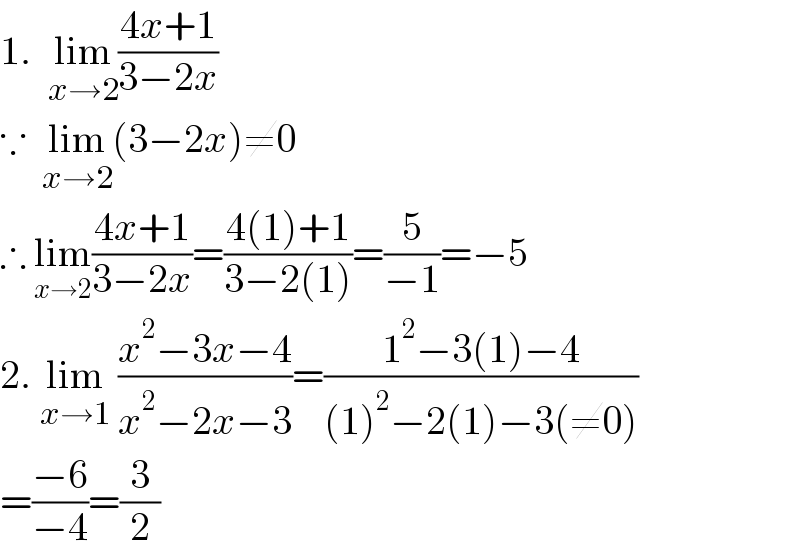
1. lim_(x→2) ((4x+1)/(3−2x)) ∵ lim_(x→2) (3−2x)≠0 ∴ lim_(x→2) ((4x+1)/(3−2x))=((4(1)+1)/(3−2(1)))=(5/(−1))=−5 2. lim_(x→1) ((x^2 −3x−4)/(x^2 −2x−3))=((1^2 −3(1)−4)/((1)^2 −2(1)−3(≠0))) =((−6)/(−4))=(3/2)

$$\mathrm{1}.\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{4}{x}+\mathrm{1}}{\mathrm{3}−\mathrm{2}{x}} \\ $$$$\because\:\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\left(\mathrm{3}−\mathrm{2}{x}\right)\neq\mathrm{0} \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\mathrm{4}{x}+\mathrm{1}}{\mathrm{3}−\mathrm{2}{x}}=\frac{\mathrm{4}\left(\mathrm{1}\right)+\mathrm{1}}{\mathrm{3}−\mathrm{2}\left(\mathrm{1}\right)}=\frac{\mathrm{5}}{−\mathrm{1}}=−\mathrm{5} \\ $$$$\mathrm{2}.\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}}{{x}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}}=\frac{\mathrm{1}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}\right)−\mathrm{4}}{\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{1}\right)−\mathrm{3}\left(\neq\mathrm{0}\right)} \\ $$$$=\frac{−\mathrm{6}}{−\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 25/Sep/22

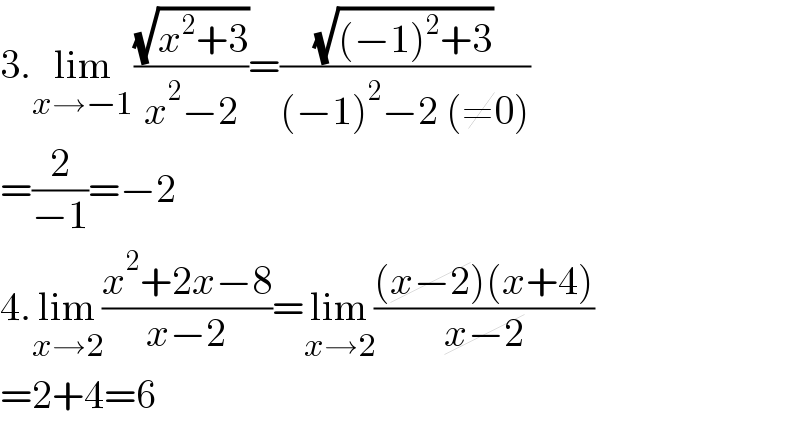
3.lim_(x→−1) ((√(x^2 +3))/(x^2 −2))=((√((−1)^2 +3))/((−1)^2 −2 (≠0))) =(2/(−1))=−2 4.lim_(x→2) ((x^2 +2x−8)/(x−2))=lim_(x→2) (((x−2)(x+4))/(x−2)) =2+4=6

$$\mathrm{3}.\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{{x}^{\mathrm{2}} −\mathrm{2}}=\frac{\sqrt{\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{3}}}{\left(−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\:\left(\neq\mathrm{0}\right)} \\ $$$$=\frac{\mathrm{2}}{−\mathrm{1}}=−\mathrm{2} \\ $$$$\mathrm{4}.\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{8}}{{x}−\mathrm{2}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\left(\cancel{{x}−\mathrm{2}}\right)\left({x}+\mathrm{4}\right)}{\cancel{{x}−\mathrm{2}}} \\ $$$$=\mathrm{2}+\mathrm{4}=\mathrm{6} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com