Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 176159 by peter frank last updated on 14/Sep/22

Answered by adhigenz last updated on 14/Sep/22

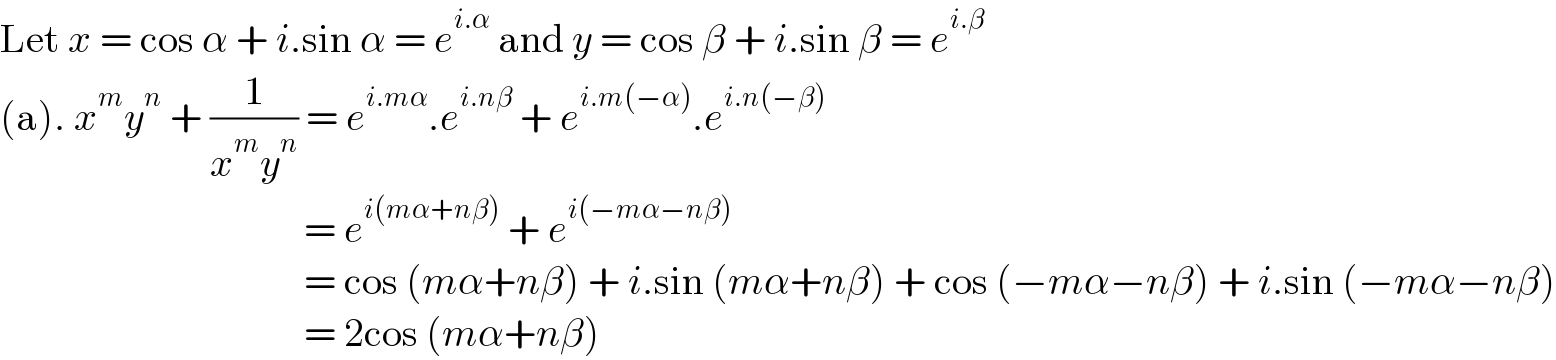
Let x = cos α + i.sin α = e^(i.α) and y = cos β + i.sin β = e^(i.β) (a). x^m y^n + (1/(x^m y^n )) = e^(i.mα) .e^(i.nβ) + e^(i.m(−α)) .e^(i.n(−β)) = e^(i(mα+nβ)) + e^(i(−mα−nβ)) = cos (mα+nβ) + i.sin (mα+nβ) + cos (−mα−nβ) + i.sin (−mα−nβ) = 2cos (mα+nβ)

$$\mathrm{Let}\:{x}\:=\:\mathrm{cos}\:\alpha\:+\:{i}.\mathrm{sin}\:\alpha\:=\:{e}^{{i}.\alpha} \:\mathrm{and}\:{y}\:=\:\mathrm{cos}\:\beta\:+\:{i}.\mathrm{sin}\:\beta\:=\:{e}^{{i}.\beta} \\ $$$$\left(\mathrm{a}\right).\:{x}^{{m}} {y}^{{n}} \:+\:\frac{\mathrm{1}}{{x}^{{m}} {y}^{{n}} }\:=\:{e}^{{i}.{m}\alpha} .{e}^{{i}.{n}\beta} \:+\:{e}^{{i}.{m}\left(−\alpha\right)} .{e}^{{i}.{n}\left(−\beta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:{e}^{{i}\left({m}\alpha+{n}\beta\right)} \:+\:{e}^{{i}\left(−{m}\alpha−{n}\beta\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{cos}\:\left({m}\alpha+{n}\beta\right)\:+\:{i}.\mathrm{sin}\:\left({m}\alpha+{n}\beta\right)\:+\:\mathrm{cos}\:\left(−{m}\alpha−{n}\beta\right)\:+\:{i}.\mathrm{sin}\:\left(−{m}\alpha−{n}\beta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2cos}\:\left({m}\alpha+{n}\beta\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com