
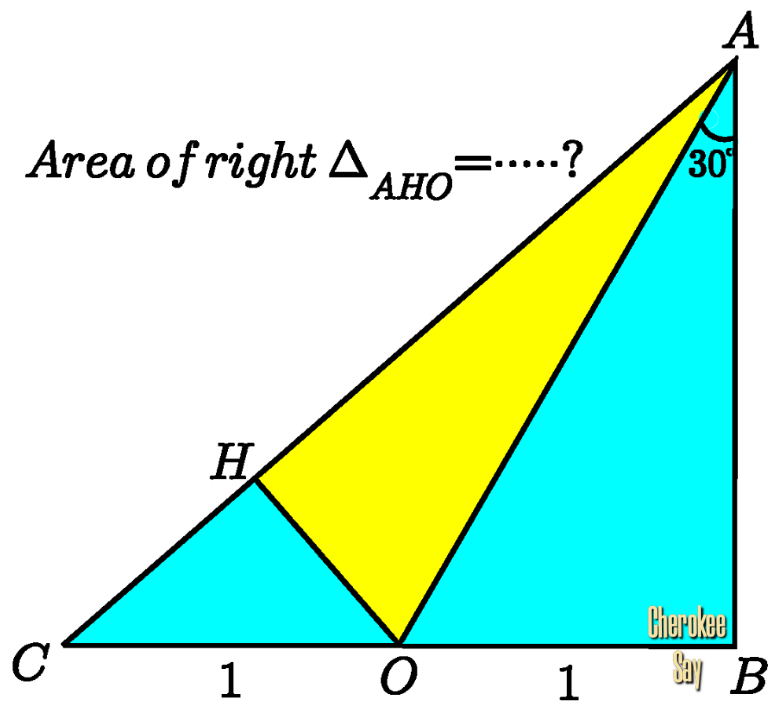
Question Number 176014 by cherokeesay last updated on 11/Sep/22
Commented by cherokeesay last updated on 11/Sep/22
$${The}\:{triangle}\:{ABC}\:{is}\:{right}-{angled}\:{at}\:{B}. \\ $$
Answered by cortano1 last updated on 11/Sep/22
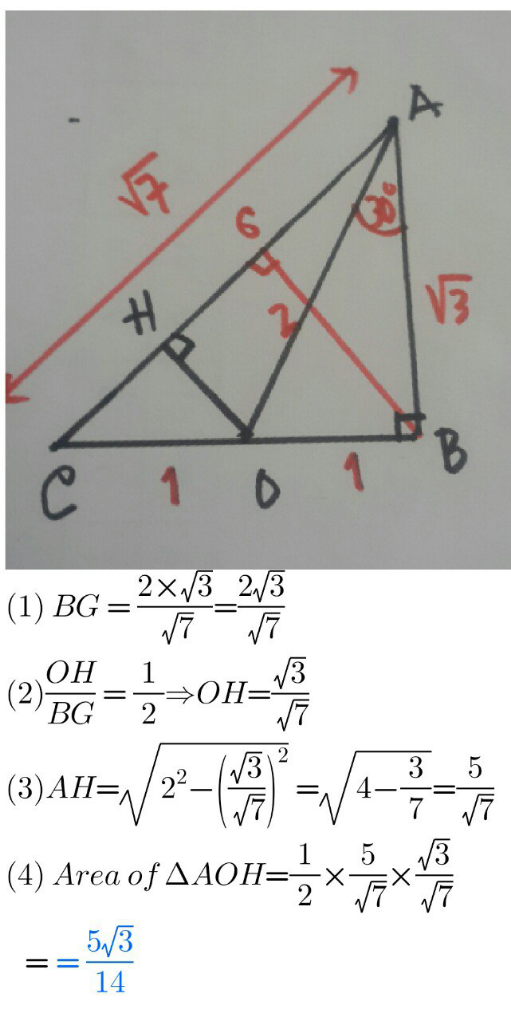
Commented by cherokeesay last updated on 11/Sep/22
$${nice}\:{thank}\:{you}\:{sir}. \\ $$
Answered by som(math1967) last updated on 11/Sep/22
![((OB)/(AB))=tan30 ⇒AB=(√(3 ))⇒ AC =(√(3+2^2 ))=(√7) △ABC∼△OHC ∴ ((area △OHC)/(area△ABC))=((OC^2 )/(AC^2 ))=(1/7) ∴ar.△OHC=(1/7)△ABC =(1/7)×(1/2)×2×(√3)=((√3)/7)sq unit ar. of △AOC=(1/2)△ABC [OC=OB] =((√3)/2) sq unit ∴ area of △AHO=((√3)/2) −((√3)/7) =((5(√3))/(14))squnit](Q176018.png)
$$\:\frac{{OB}}{{AB}}={tan}\mathrm{30} \\ $$$$\Rightarrow{AB}=\sqrt{\mathrm{3}\:}\Rightarrow\:{AC}\:=\sqrt{\mathrm{3}+\mathrm{2}^{\mathrm{2}} }=\sqrt{\mathrm{7}} \\ $$$$\bigtriangleup{ABC}\sim\bigtriangleup{OHC} \\ $$$$\:\therefore\:\:\frac{{area}\:\bigtriangleup{OHC}}{{area}\bigtriangleup{ABC}}=\frac{{OC}^{\mathrm{2}} }{{AC}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\therefore{ar}.\bigtriangleup{OHC}=\frac{\mathrm{1}}{\mathrm{7}}\bigtriangleup{ABC} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7}}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\sqrt{\mathrm{3}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{7}}{sq}\:{unit} \\ $$$${ar}.\:{of}\:\bigtriangleup{AOC}=\frac{\mathrm{1}}{\mathrm{2}}\bigtriangleup{ABC}\:\left[{OC}={OB}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:{sq}\:{unit} \\ $$$$\therefore\:{area}\:{of}\:\bigtriangleup{AHO}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:−\frac{\sqrt{\mathrm{3}}}{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}}{squnit} \\ $$$$\: \\ $$
Commented by cortano1 last updated on 11/Sep/22
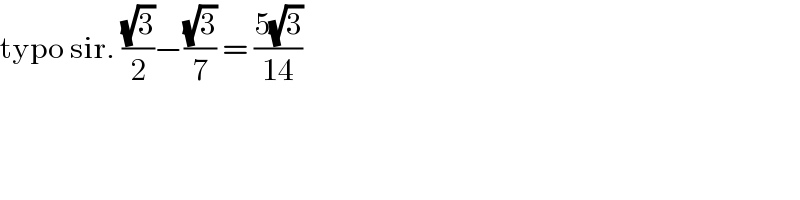
$$\mathrm{typo}\:\mathrm{sir}.\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{7}}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}} \\ $$
Commented by som(math1967) last updated on 11/Sep/22
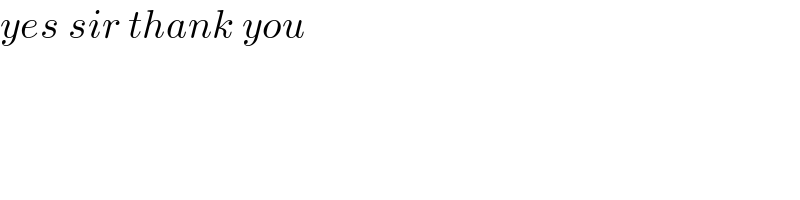
$${yes}\:{sir}\:{thank}\:{you} \\ $$
Commented by cherokeesay last updated on 11/Sep/22

$${thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 11/Sep/22
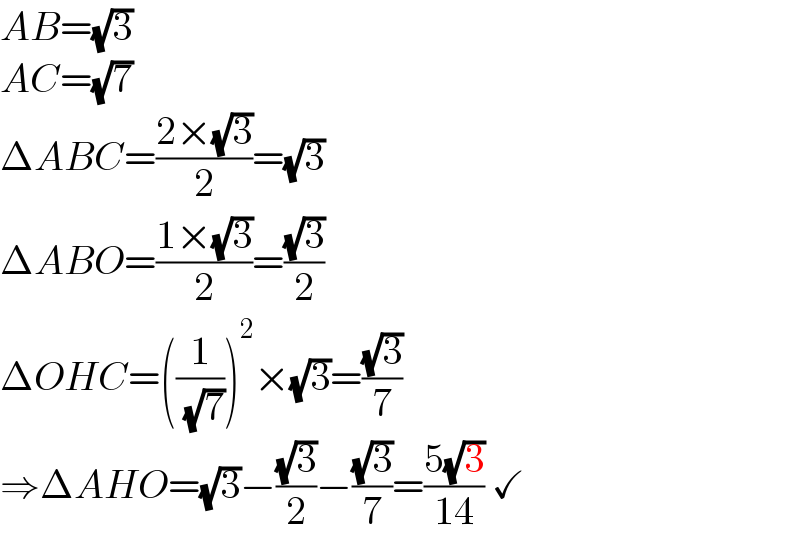
$${AB}=\sqrt{\mathrm{3}} \\ $$$${AC}=\sqrt{\mathrm{7}} \\ $$$$\Delta{ABC}=\frac{\mathrm{2}×\sqrt{\mathrm{3}}}{\mathrm{2}}=\sqrt{\mathrm{3}} \\ $$$$\Delta{ABO}=\frac{\mathrm{1}×\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Delta{OHC}=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{7}}}\right)^{\mathrm{2}} ×\sqrt{\mathrm{3}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{7}} \\ $$$$\Rightarrow\Delta{AHO}=\sqrt{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{7}}=\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{14}}\:\checkmark \\ $$
Commented by cortano1 last updated on 11/Sep/22

$$\mathrm{why}\:\sqrt{\mathrm{5}}\:? \\ $$
Commented by mr W last updated on 11/Sep/22

$${typo} \\ $$
Commented by cherokeesay last updated on 11/Sep/22

$${thank}\:{you}\:{sir}. \\ $$
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
