
Question Number 17600 by mondodotto@gmail.com last updated on 08/Jul/17
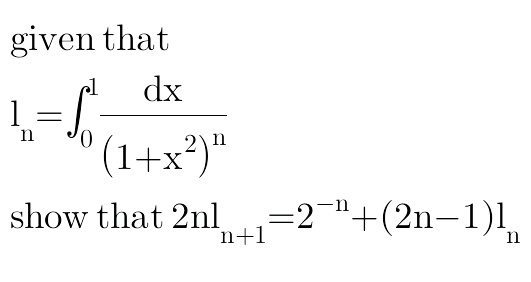
Answered by alex041103 last updated on 08/Jul/17
![We use the following trig sub: x=tan(θ)⇒dx=sec^2 (θ)dθ We know that 1+tan^2 θ=sec^2 θ ⇒(dx/((1+x^2 )^n ))=((sec^2 θ dθ)/(sec^(2n) θ))=(dθ/(sec^(2(n−1)) θ)) But (1/(sec x))=cos x ⇒ (dθ/(sec^(2(n−1)) θ))=cos^(2(n−1)) θ dθ Now we change the limits of integration: x=tanθ⇒θ=tan^(−1) x ⇒I_n =∫_(tan^(−1) (0)) ^(tan^(−1) (1)) cos^(2(n−1)) θ dθ = ∫_( 0) ^(π/4) cos^(2(n−1)) θ dθ ⇒I_(n+1) =∫_0 ^(π/4) cos^(2n) θ dθ Now we use integration by parts: I_(n+1) =∫_0 ^(π/4) cos^(2n−1) θ cosθ dθ u=cos^(2n−1) θ⇒du=(2n−1)cos^(2(n−1)) θ(−sinθ) dv=cosθdθ⇒v=sinθ ∫_a ^b u dv=(uv)_a ^b − ∫_a ^b v du ⇒I_(n+1) =∫_0 ^(π/4) cos^(2n−1) θ cosθ dθ= =(cos^(2n−1) θsinθ)_0 ^(π/4) + (2n−1)∫_0 ^(π/4) sin^2 θcos^(2(n−1)) θ dθ For (cos^(2n−1) θsinθ)_0 ^(π/4) we have: (cos^(2n−1) θsinθ)_0 ^(π/4) = (((√2)/2))^(2n−1) (((√2)/2)) −(1)^(2n−1) (0) =((1/(√2)))^(2n) =(1/2^n )=2^(−n) Let substitute sin^2 θ=1−cos^2 θ I_(n+1) =2^(−n) + (2n−1)∫_0 ^(π/4) (1−cos^2 θ)cos^(2(n−1)) θ dθ= =2^(−n) +(2n−1)[∫_0 ^(π/4) cos^(2(n−1)) θ dθ − ∫_0 ^(π/4) cos^(2n) θ dθ] But ∫_0 ^(π/4) cos^(2(n−1)) θ dθ = I_n and ∫_0 ^(π/4) cos^(2n) θ dθ = I_(n+1) ⇒I_(n+1) = 2^(−n) + (2n−1)(I_n − I_(n+1) ) I_(n+1) = 2^(−n) + (2n−1)I_n − (2n−1)I_(n+1) ⇒ 2nI_(n+1) = 2^(−n) + (2n−1)I_n Any questions?](Q17605.png)
$$\mathrm{We}\:\mathrm{use}\:\mathrm{the}\:\mathrm{following}\:\mathrm{trig}\:\mathrm{sub}: \\ $$$${x}={tan}\left(\theta\right)\Rightarrow{dx}={sec}^{\mathrm{2}} \left(\theta\right){d}\theta \\ $$$$\mathrm{We}\:\mathrm{know}\:\mathrm{that}\:\mathrm{1}+{tan}^{\mathrm{2}} \theta={sec}^{\mathrm{2}} \theta \\ $$$$\Rightarrow\frac{{dx}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} }=\frac{{sec}^{\mathrm{2}} \theta\:{d}\theta}{{sec}^{\mathrm{2}{n}} \theta}=\frac{{d}\theta}{{sec}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta} \\ $$$$\mathrm{But}\:\frac{\mathrm{1}}{\mathrm{sec}\:\mathrm{x}}=\mathrm{cos}\:\mathrm{x} \\ $$$$\Rightarrow\:\frac{{d}\theta}{{sec}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta}={cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{change}\:\mathrm{the}\:\mathrm{limits}\:\mathrm{of}\:\mathrm{integration}: \\ $$$${x}={tan}\theta\Rightarrow\theta={tan}^{−\mathrm{1}} {x} \\ $$$$\Rightarrow\mathrm{I}_{{n}} =\underset{{tan}^{−\mathrm{1}} \left(\mathrm{0}\right)} {\overset{{tan}^{−\mathrm{1}} \left(\mathrm{1}\right)} {\int}}{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta \\ $$$$=\:\underset{\:\:\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta \\ $$$$\Rightarrow\mathrm{I}_{{n}+\mathrm{1}} =\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}{n}} \theta\:{d}\theta \\ $$$$\mathrm{Now}\:\mathrm{we}\:\mathrm{use}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{parts}: \\ $$$$\mathrm{I}_{{n}+\mathrm{1}} =\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}{n}−\mathrm{1}} \theta\:\mathrm{cos}\theta\:{d}\theta \\ $$$${u}={cos}^{\mathrm{2}{n}−\mathrm{1}} \theta\Rightarrow{du}=\left(\mathrm{2}{n}−\mathrm{1}\right){cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\left(−{sin}\theta\right) \\ $$$${dv}={cos}\theta{d}\theta\Rightarrow{v}={sin}\theta \\ $$$$\underset{{a}} {\overset{{b}} {\int}}{u}\:{dv}=\left({uv}\underset{{a}} {\overset{{b}} {\right)}}\:−\:\underset{{a}} {\overset{{b}} {\int}}{v}\:{du} \\ $$$$\Rightarrow\mathrm{I}_{{n}+\mathrm{1}} =\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}{n}−\mathrm{1}} \theta\:\mathrm{cos}\theta\:{d}\theta= \\ $$$$\:=\left({cos}^{\mathrm{2}{n}−\mathrm{1}} \theta{sin}\theta\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\right)}}\:+\:\left(\mathrm{2}{n}−\mathrm{1}\right)\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{sin}^{\mathrm{2}} \theta{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta \\ $$$$\mathrm{For}\:\left({cos}^{\mathrm{2}{n}−\mathrm{1}} \theta{sin}\theta\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\right)}}\:\mathrm{we}\:\mathrm{have}: \\ $$$$\left({cos}^{\mathrm{2}{n}−\mathrm{1}} \theta{sin}\theta\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\right)}}\:=\:\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}{n}−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)\:−\left(\mathrm{1}\right)^{\mathrm{2}{n}−\mathrm{1}} \left(\mathrm{0}\right) \\ $$$$=\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}{n}} =\frac{\mathrm{1}}{\mathrm{2}^{{n}} }=\mathrm{2}^{−{n}} \\ $$$$\mathrm{Let}\:\mathrm{substitute}\:{sin}^{\mathrm{2}} \theta=\mathrm{1}−{cos}^{\mathrm{2}} \theta \\ $$$$\:\mathrm{I}_{{n}+\mathrm{1}} =\mathrm{2}^{−{n}} \:+\:\left(\mathrm{2}{n}−\mathrm{1}\right)\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\left(\mathrm{1}−{cos}^{\mathrm{2}} \theta\right){cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta= \\ $$$$=\mathrm{2}^{−{n}} +\left(\mathrm{2}{n}−\mathrm{1}\right)\left[\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta\:\:−\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}{n}} \theta\:{d}\theta\right] \\ $$$$\mathrm{But}\: \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \theta\:{d}\theta\:=\:\mathrm{I}_{{n}} \:\mathrm{and} \\ $$$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}{cos}^{\mathrm{2}{n}} \theta\:{d}\theta\:=\:\mathrm{I}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{−{n}} \:+\:\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{I}_{{n}} \:−\:\mathrm{I}_{{n}+\mathrm{1}} \right) \\ $$$$\:\:\:\:\:\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{−{n}} \:+\:\left(\mathrm{2}{n}−\mathrm{1}\right)\mathrm{I}_{{n}} \:−\:\left(\mathrm{2}{n}−\mathrm{1}\right)\mathrm{I}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{2}{n}\mathrm{I}_{{n}+\mathrm{1}} \:=\:\mathrm{2}^{−{n}} \:+\:\left(\mathrm{2}{n}−\mathrm{1}\right)\mathrm{I}_{{n}} \\ $$$${Any}\:{questions}? \\ $$
