
Question Number 175949 by mr W last updated on 10/Sep/22
Commented by mr W last updated on 10/Sep/22

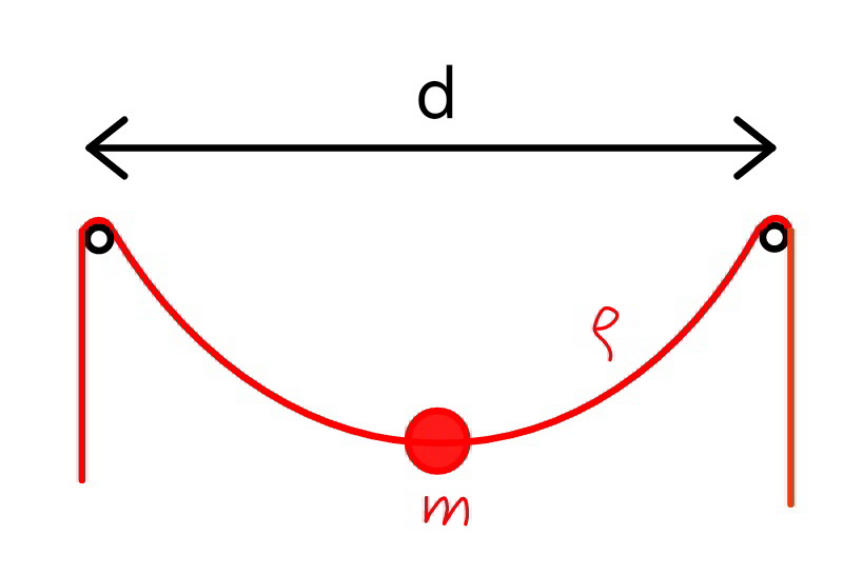
$${a}\:{mass}\:{m}\:{is}\:{fixed}\:{at}\:{the}\:{midpoint} \\ $$$${of}\:{an}\:{uniform}\:{thin}\:{rope}\:{with}\:{unit}\: \\ $$$${mass}\:\rho.\:{find}\:{the}\:{minimum}\:{length}\:{of} \\ $$$${the}\:{rope}\:{such}\:{that}\:{it}\:{can}\:{be}\:{kept}\:{in}\: \\ $$$${equilibrium}\:{as}\:{shown}.\: \\ $$$$\left({no}\:{friction}\right) \\ $$$${as}\:{example}:\:{m}=\rho{d} \\ $$
Answered by mr W last updated on 14/Sep/22

Commented by mr W last updated on 11/Sep/22
Commented by mr W last updated on 13/Sep/22
![let L=total length of the rope say length of rope part BC is h, then the length of part AB=(L/2)−h AB is a segment of a catenary. T_2 =hρg T_1 sin θ_1 =((mg)/2) T_0 =T_2 cos θ_2 =T_1 cos θ_1 with a=(T_0 /(ρg)) the eqn. of the catenary is: y=a cosh (x/a) tan θ=y′=sinh (x/a) s=a sinh (x/a) at point A: tan θ_1 =sinh (d_1 /a) s_1 =a sinh (d_1 /a) at point B: tan θ_2 =sinh ((d_1 +(d/2))/a) s_2 =a sinh ((d_1 +(d/2))/a) T_0 =T_1 cos θ_1 aρg=((mg)/(2 tan θ_1 )) tan θ_1 =(m/(2ρa)) sinh (d_1 /a)=(m/(2ρa)) ⇒(d_1 /a)=sinh^(−1) (m/(2ρa)) T_0 =T_2 cos θ_2 aρg=hρg cos θ_2 cos θ_2 =(a/h) ⇒tan θ_2 =((√(1−((a/h))^2 ))/(a/h)) tan θ_2 =sinh ((d_1 +(d/2))/a)=((√(1−((a/h))^2 ))/(a/h)) ⇒((d_1 +(d/2))/a)=sinh^(−1) ((√(1−((a/h))^2 ))/(a/h)) ⇒(d/(2a))+sinh^(−1) (m/(2ρa))=sinh^(−1) ((√(1−((a/h))^2 ))/(a/h)) let k=(m/(ρd)), η=(a/h), ξ=(d/(2a)) ⇒ξ+sinh^(−1) (kξ)=sinh^(−1) ((√(1−η^2 ))/η) ⇒((√(1−η^2 ))/η)=sinh [ξ+sinh^(−1) (kξ)] ⇒η=(1/( (√(1+sinh^2 [ξ+sinh^(−1) (kξ)])))) s_2 −s_1 =(L/2)−h a(sinh ((d_1 +(d/2))/a)−sinh (d_1 /a))=(L/2)−h a(((√(1−((a/h))^2 ))/(a/h))−(m/(2ρa)))=(L/2)−h L+(m/ρ)=2h[1+(√(1−((a/h))^2 ))] Φ=(L/d)+k=((1+(√(1−η^2 )))/(ηξ)) Φ=((sinh [ξ+sinh^(−1) (kξ)]+(√(1+sinh^2 [ξ+sinh^(−1) (kξ)])))/ξ) minimum L ⇔ (dΦ/dξ)=0 λ=(h/d)=(1/(2ηξ))=((√(1+sinh^2 [ξ+sinh^(−1) (kξ)]))/(2ξ)) examples: m=0 ⇒k=0: Φ_(min) =e ⇒L_(min) =ed m=ρd ⇒k=1: Φ_(min) =5.3268 ⇒L_(min) =4.3268d m=2ρd ⇒k=2: Φ_(min) =7.7568 ⇒L_(min) =5.7568d](Q176038.png)
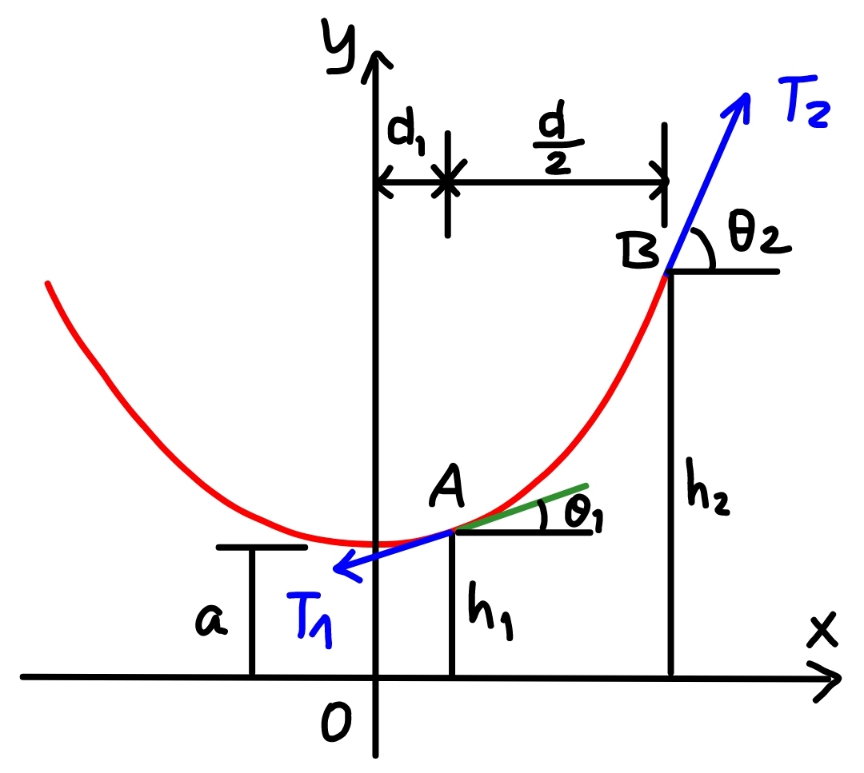
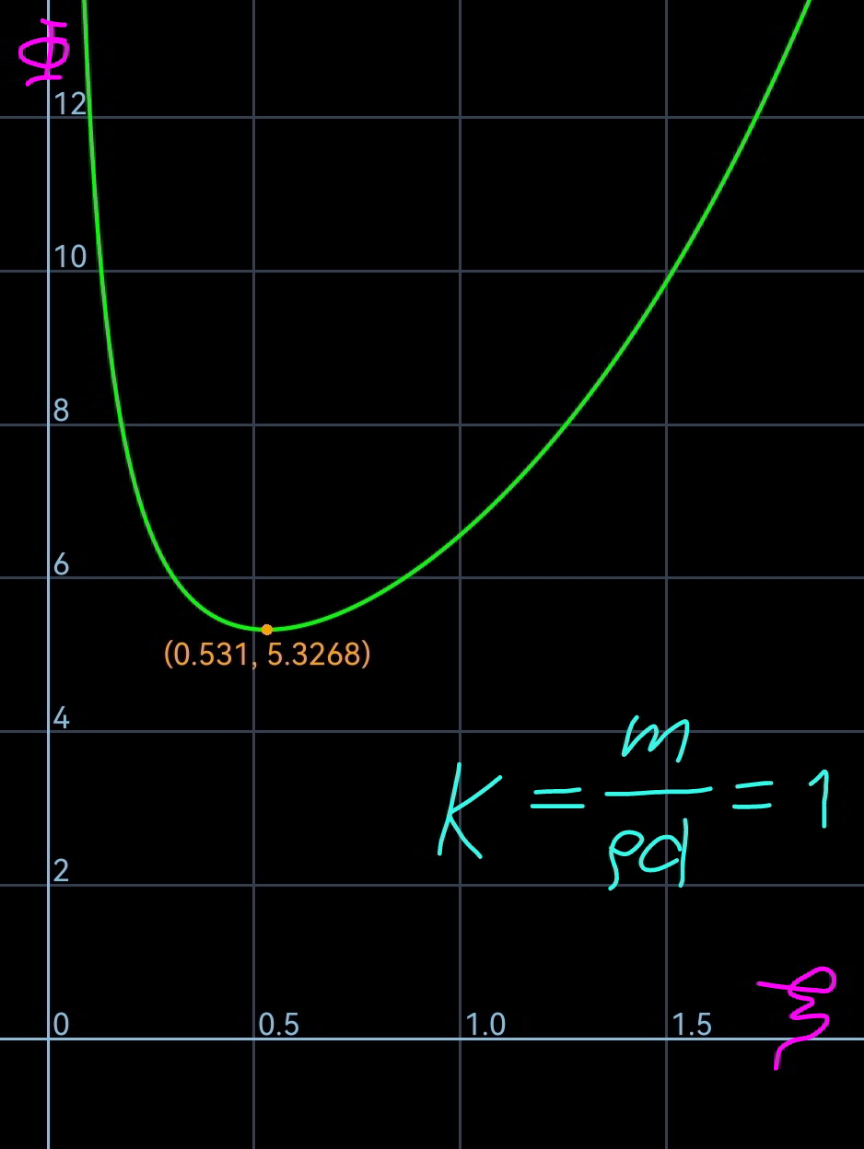
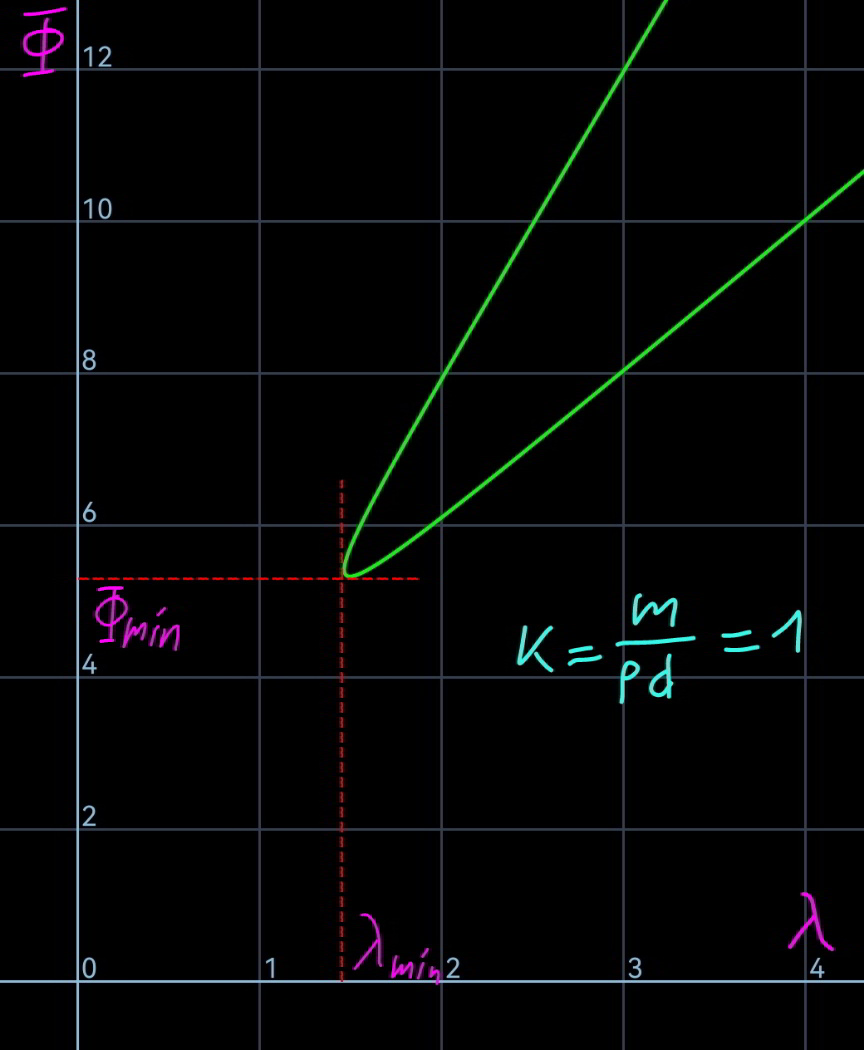
$${let}\:{L}={total}\:{length}\:{of}\:{the}\:{rope} \\ $$$${say}\:{length}\:{of}\:{rope}\:{part}\:{BC}\:{is}\:{h}, \\ $$$${then}\:{the}\:{length}\:{of}\:{part}\:{AB}=\frac{{L}}{\mathrm{2}}−{h} \\ $$$${AB}\:{is}\:{a}\:{segment}\:{of}\:{a}\:{catenary}. \\ $$$${T}_{\mathrm{2}} ={h}\rho{g} \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} =\frac{{mg}}{\mathrm{2}} \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{2}} \mathrm{cos}\:\theta_{\mathrm{2}} ={T}_{\mathrm{1}} \mathrm{cos}\:\theta_{\mathrm{1}} \\ $$$$ \\ $$$${with}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}\:{the}\:{eqn}.\:{of}\:{the}\:{catenary}\:{is}: \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$${s}={a}\:\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{A}: \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} =\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}} \\ $$$${s}_{\mathrm{1}} ={a}\:\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{B}: \\ $$$$\mathrm{tan}\:\theta_{\mathrm{2}} =\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +\frac{{d}}{\mathrm{2}}}{{a}} \\ $$$${s}_{\mathrm{2}} ={a}\:\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +\frac{{d}}{\mathrm{2}}}{{a}} \\ $$$$ \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{1}} \mathrm{cos}\:\theta_{\mathrm{1}} \\ $$$${a}\rho{g}=\frac{{mg}}{\mathrm{2}\:\mathrm{tan}\:\theta_{\mathrm{1}} } \\ $$$$\mathrm{tan}\:\theta_{\mathrm{1}} =\frac{{m}}{\mathrm{2}\rho{a}} \\ $$$$\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}}=\frac{{m}}{\mathrm{2}\rho{a}} \\ $$$$\Rightarrow\frac{{d}_{\mathrm{1}} }{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{{m}}{\mathrm{2}\rho{a}} \\ $$$$ \\ $$$${T}_{\mathrm{0}} ={T}_{\mathrm{2}} \mathrm{cos}\:\theta_{\mathrm{2}} \\ $$$${a}\rho{g}={h}\rho{g}\:\mathrm{cos}\:\theta_{\mathrm{2}} \\ $$$$\mathrm{cos}\:\theta_{\mathrm{2}} =\frac{{a}}{{h}}\:\Rightarrow\mathrm{tan}\:\theta_{\mathrm{2}} =\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }}{\frac{{a}}{{h}}} \\ $$$$\mathrm{tan}\:\theta_{\mathrm{2}} =\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +\frac{{d}}{\mathrm{2}}}{{a}}=\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }}{\frac{{a}}{{h}}} \\ $$$$\Rightarrow\frac{{d}_{\mathrm{1}} +\frac{{d}}{\mathrm{2}}}{{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }}{\frac{{a}}{{h}}} \\ $$$$\Rightarrow\frac{{d}}{\mathrm{2}{a}}+\mathrm{sinh}^{−\mathrm{1}} \:\frac{{m}}{\mathrm{2}\rho{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }}{\frac{{a}}{{h}}} \\ $$$${let}\:{k}=\frac{{m}}{\rho{d}},\:\eta=\frac{{a}}{{h}},\:\xi=\frac{{d}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\eta} \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\eta}=\mathrm{sinh}\:\left[\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)\right] \\ $$$$\Rightarrow\eta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \:\left[\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)\right]}} \\ $$$$ \\ $$$${s}_{\mathrm{2}} −{s}_{\mathrm{1}} =\frac{{L}}{\mathrm{2}}−{h} \\ $$$${a}\left(\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} +\frac{{d}}{\mathrm{2}}}{{a}}−\mathrm{sinh}\:\frac{{d}_{\mathrm{1}} }{{a}}\right)=\frac{{L}}{\mathrm{2}}−{h} \\ $$$${a}\left(\frac{\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }}{\frac{{a}}{{h}}}−\frac{{m}}{\mathrm{2}\rho{a}}\right)=\frac{{L}}{\mathrm{2}}−{h} \\ $$$${L}+\frac{{m}}{\rho}=\mathrm{2}{h}\left[\mathrm{1}+\sqrt{\mathrm{1}−\left(\frac{{a}}{{h}}\right)^{\mathrm{2}} }\right] \\ $$$$\Phi=\frac{{L}}{{d}}+{k}=\frac{\mathrm{1}+\sqrt{\mathrm{1}−\eta^{\mathrm{2}} }}{\eta\xi} \\ $$$$\Phi=\frac{\mathrm{sinh}\:\left[\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)\right]+\sqrt{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \:\left[\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)\right]}}{\xi} \\ $$$${minimum}\:{L}\:\Leftrightarrow\:\:\frac{{d}\Phi}{{d}\xi}=\mathrm{0} \\ $$$$ \\ $$$$\lambda=\frac{{h}}{{d}}=\frac{\mathrm{1}}{\mathrm{2}\eta\xi}=\frac{\sqrt{\mathrm{1}+\mathrm{sinh}^{\mathrm{2}} \:\left[\xi+\mathrm{sinh}^{−\mathrm{1}} \:\left({k}\xi\right)\right]}}{\mathrm{2}\xi} \\ $$$$ \\ $$$$\underline{{examples}:} \\ $$$${m}=\mathrm{0}\:\Rightarrow{k}=\mathrm{0}: \\ $$$$\Phi_{{min}} ={e}\:\Rightarrow{L}_{{min}} ={ed} \\ $$$$ \\ $$$${m}=\rho{d}\:\Rightarrow{k}=\mathrm{1}: \\ $$$$\Phi_{{min}} =\mathrm{5}.\mathrm{3268}\:\Rightarrow{L}_{{min}} =\mathrm{4}.\mathrm{3268}{d} \\ $$$$ \\ $$$${m}=\mathrm{2}\rho{d}\:\Rightarrow{k}=\mathrm{2}: \\ $$$$\Phi_{{min}} =\mathrm{7}.\mathrm{7568}\:\Rightarrow{L}_{{min}} =\mathrm{5}.\mathrm{7568}{d} \\ $$
Commented by mr W last updated on 11/Sep/22
Commented by mr W last updated on 11/Sep/22
Commented by Tawa11 last updated on 15/Sep/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
