Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 175588 by alcohol last updated on 03/Sep/22

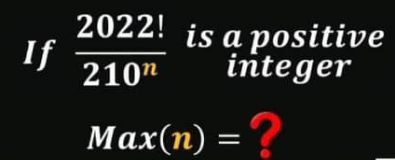
Commented by mahdipoor last updated on 04/Oct/22

210=2×3×5×7 in 2022!=2^a ×3^b ×5^c ×7^d ×... a≥b≥c≥d≥... ⇒ max(n) if ((2022!)/(210^n ))∈N = max(d) if ((2022!)/7^d )∈N d=[((2022)/7)]+[((2022)/7^2 )]+[((2022)/7^3 )]+[((2022)/7^4 )]+...= 288+41+5+0+...=334

$$\mathrm{210}=\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7} \\ $$$${in}\:\mathrm{2022}!=\mathrm{2}^{{a}} ×\mathrm{3}^{{b}} ×\mathrm{5}^{{c}} ×\mathrm{7}^{{d}} ×... \\ $$$${a}\geqslant{b}\geqslant{c}\geqslant{d}\geqslant...\:\Rightarrow \\ $$$${max}\left({n}\right)\:{if}\:\frac{\mathrm{2022}!}{\mathrm{210}^{{n}} }\in{N}\:=\:{max}\left({d}\right)\:{if}\:\frac{\mathrm{2022}!}{\mathrm{7}^{{d}} }\in{N} \\ $$$${d}=\left[\frac{\mathrm{2022}}{\mathrm{7}}\right]+\left[\frac{\mathrm{2022}}{\mathrm{7}^{\mathrm{2}} }\right]+\left[\frac{\mathrm{2022}}{\mathrm{7}^{\mathrm{3}} }\right]+\left[\frac{\mathrm{2022}}{\mathrm{7}^{\mathrm{4}} }\right]+...= \\ $$$$\mathrm{288}+\mathrm{41}+\mathrm{5}+\mathrm{0}+...=\mathrm{334} \\ $$

Answered by BaliramKumar last updated on 13/Mar/23

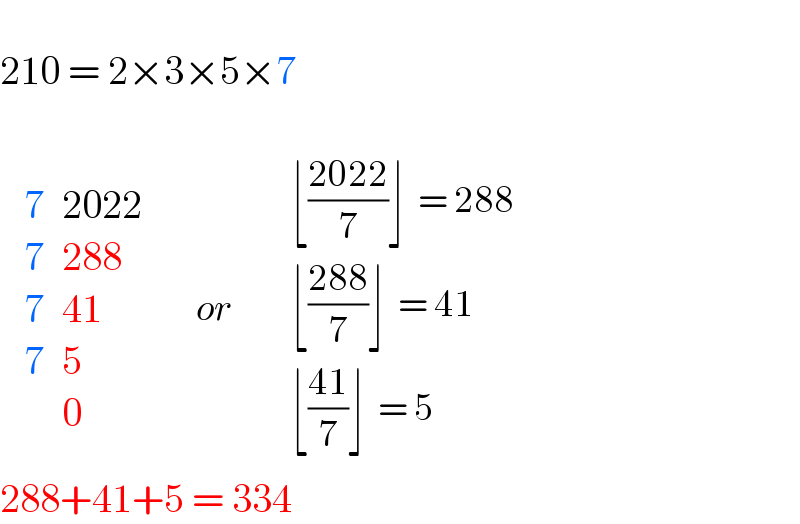
210 = 2×3×5×7 determinant ((7,(2022)),(7,(288)),(7,(41)),(7,5),(,0)) or determinant (((⌊((2022)/7)⌋ = 288)),((⌊((288)/7)⌋ = 41)),((⌊((41)/7)⌋ = 5))) 288+41+5 = 334

$$ \\ $$$$\mathrm{210}\:=\:\mathrm{2}×\mathrm{3}×\mathrm{5}×\mathrm{7} \\ $$$$ \\ $$$$\:\begin{array}{|c|c|c|c|c|}{\mathrm{7}}&\hline{\mathrm{2022}}\\{\mathrm{7}}&\hline{\mathrm{288}}\\{\mathrm{7}}&\hline{\mathrm{41}}\\{\mathrm{7}}&\hline{\mathrm{5}}\\{}&\hline{\mathrm{0}}\\\hline\end{array}\:\:\:\:\:\:{or}\:\:\:\:\:\:\:\begin{array}{|c|c|c|}{\lfloor\frac{\mathrm{2022}}{\mathrm{7}}\rfloor\:\:=\:\mathrm{288}}\\{\lfloor\frac{\mathrm{288}}{\mathrm{7}}\rfloor\:\:=\:\mathrm{41}}\\{\lfloor\frac{\mathrm{41}}{\mathrm{7}}\rfloor\:\:=\:\mathrm{5}}\\\hline\end{array} \\ $$$$\mathrm{288}+\mathrm{41}+\mathrm{5}\:=\:\mathrm{334} \\ $$

Commented by Tawa11 last updated on 15/Sep/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 03/Sep/22

((2022!)/(210^n ))=k 2022!=210^n k 2022!=2^n 3^n 5^n 7^n k 2022!=2^(2014) ×3^(1006) ×5^(503) ×7^(334) ×... ⇒n_(max) =334 see also Q115294

$$\frac{\mathrm{2022}!}{\mathrm{210}^{{n}} }={k} \\ $$$$\mathrm{2022}!=\mathrm{210}^{{n}} {k} \\ $$$$\mathrm{2022}!=\mathrm{2}^{{n}} \mathrm{3}^{{n}} \mathrm{5}^{{n}} \mathrm{7}^{{n}} {k} \\ $$$$\mathrm{2022}!=\mathrm{2}^{\mathrm{2014}} ×\mathrm{3}^{\mathrm{1006}} ×\mathrm{5}^{\mathrm{503}} ×\mathrm{7}^{\mathrm{334}} ×... \\ $$$$\Rightarrow{n}_{{max}} =\mathrm{334} \\ $$$${see}\:{also}\:{Q}\mathrm{115294} \\ $$

Commented by Tawa11 last updated on 15/Sep/22

Great sir

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com