
Question Number 173240 by mnjuly1970 last updated on 08/Jul/22
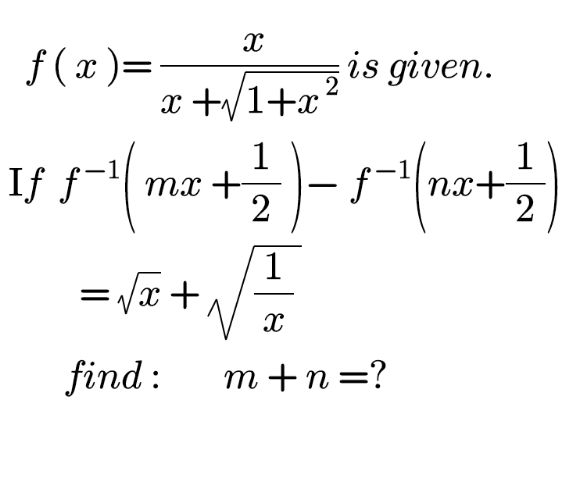
Commented by a.lgnaoui last updated on 09/Jul/22

Commented by a.lgnaoui last updated on 09/Jul/22
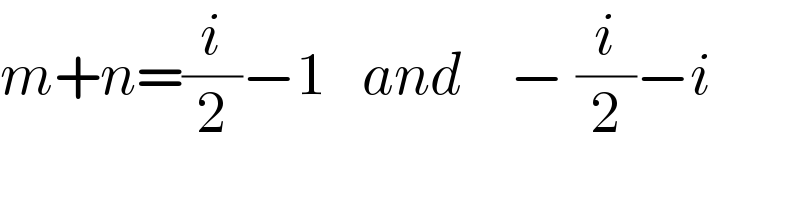
$${m}+{n}=\frac{{i}}{\mathrm{2}}−\mathrm{1}\:\:\:{and}\:\:\:\:−\:\frac{{i}}{\mathrm{2}}−{i} \\ $$
Answered by mr W last updated on 09/Jul/22
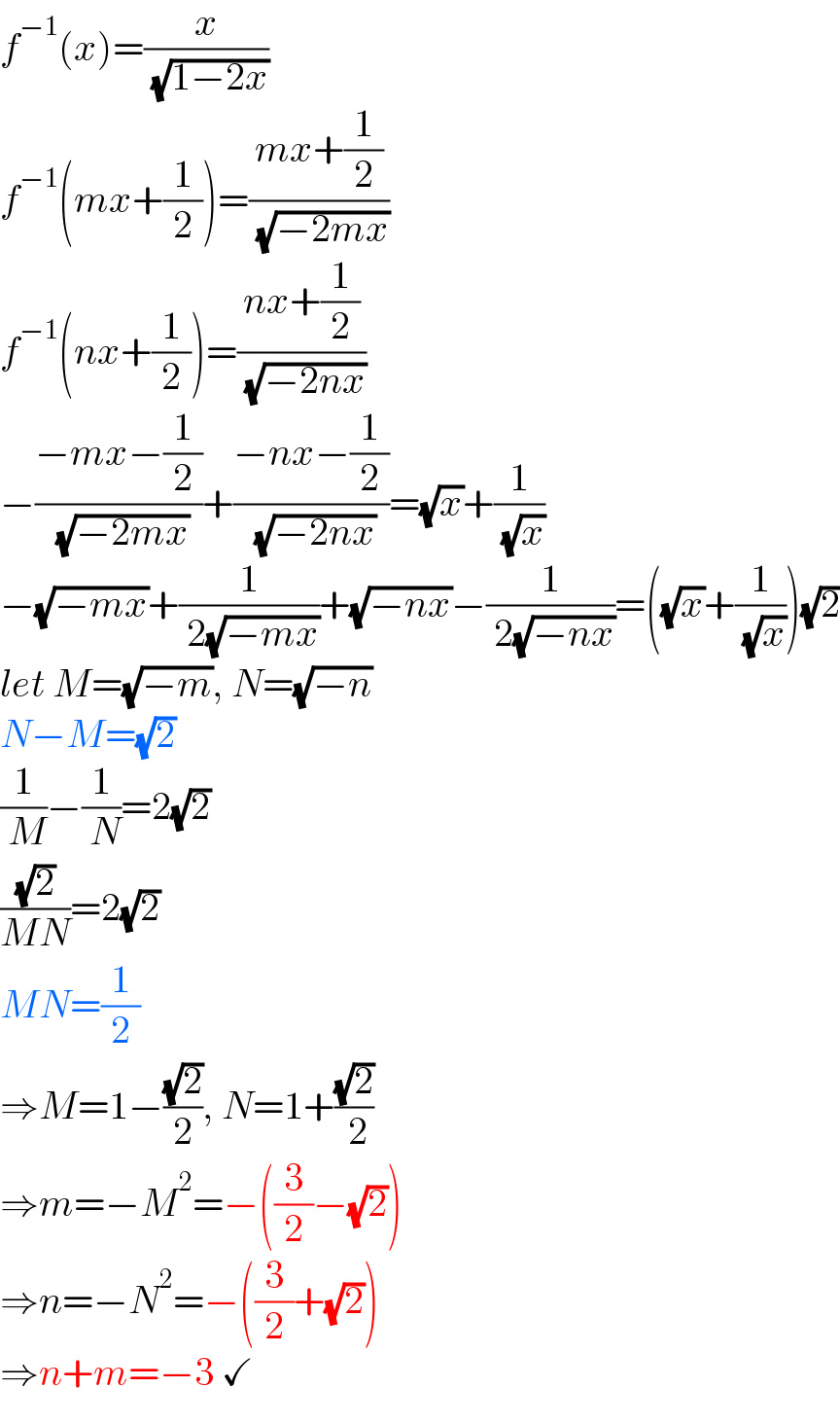
$${f}^{−\mathrm{1}} \left({x}\right)=\frac{{x}}{\:\sqrt{\mathrm{1}−\mathrm{2}{x}}} \\ $$$${f}^{−\mathrm{1}} \left({mx}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{{mx}+\frac{\mathrm{1}}{\mathrm{2}}}{\:\sqrt{−\mathrm{2}{mx}}} \\ $$$${f}^{−\mathrm{1}} \left({nx}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{{nx}+\frac{\mathrm{1}}{\mathrm{2}}}{\:\sqrt{−\mathrm{2}{nx}}} \\ $$$$−\frac{−{mx}−\frac{\mathrm{1}}{\mathrm{2}}}{\:\sqrt{−\mathrm{2}{mx}}}+\frac{−{nx}−\frac{\mathrm{1}}{\mathrm{2}}}{\:\sqrt{−\mathrm{2}{nx}}}=\sqrt{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}} \\ $$$$−\sqrt{−{mx}}+\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{−{mx}}}+\sqrt{−{nx}}−\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{−{nx}}}=\left(\sqrt{{x}}+\frac{\mathrm{1}}{\:\sqrt{{x}}}\right)\sqrt{\mathrm{2}} \\ $$$${let}\:{M}=\sqrt{−{m}},\:{N}=\sqrt{−{n}} \\ $$$${N}−{M}=\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\:{M}}−\frac{\mathrm{1}}{\:{N}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\frac{\sqrt{\mathrm{2}}}{{MN}}=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${MN}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{M}=\mathrm{1}−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}},\:{N}=\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\:\mathrm{2}} \\ $$$$\Rightarrow{m}=−{M}^{\mathrm{2}} =−\left(\frac{\mathrm{3}}{\mathrm{2}}−\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{n}=−{N}^{\mathrm{2}} =−\left(\frac{\mathrm{3}}{\mathrm{2}}+\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{n}+{m}=−\mathrm{3}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 09/Jul/22
$$\mathrm{thanks}\:\mathrm{alot}\:\mathrm{sir}\:\mathrm{W} \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
