
Question Number 172956 by dragan91 last updated on 03/Jul/22
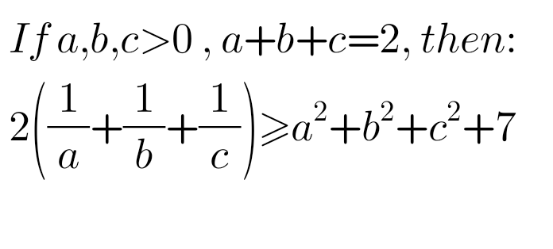
Commented by Shrinava last updated on 04/Jul/22
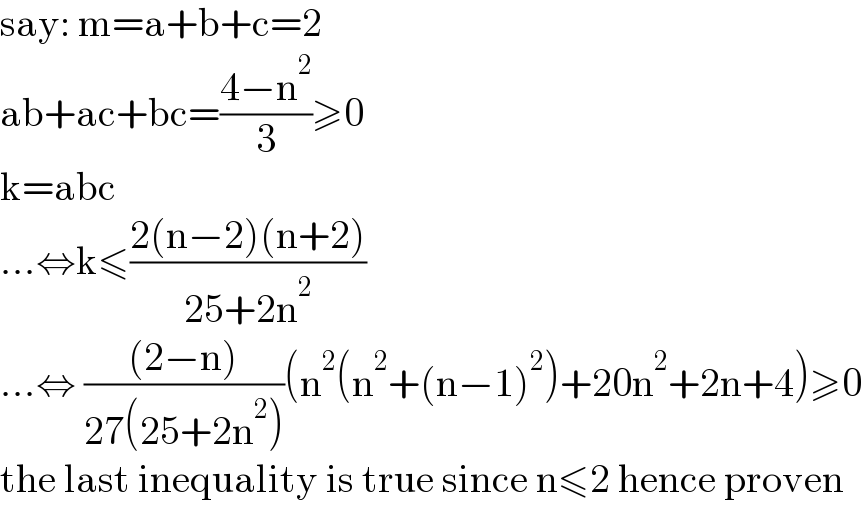
$$\mathrm{say}:\:\mathrm{m}=\mathrm{a}+\mathrm{b}+\mathrm{c}=\mathrm{2} \\ $$$$\mathrm{ab}+\mathrm{ac}+\mathrm{bc}=\frac{\mathrm{4}−\mathrm{n}^{\mathrm{2}} }{\mathrm{3}}\geqslant\mathrm{0} \\ $$$$\mathrm{k}=\mathrm{abc} \\ $$$$...\Leftrightarrow\mathrm{k}\leqslant\frac{\mathrm{2}\left(\mathrm{n}−\mathrm{2}\right)\left(\mathrm{n}+\mathrm{2}\right)}{\mathrm{25}+\mathrm{2n}^{\mathrm{2}} } \\ $$$$...\Leftrightarrow\:\frac{\left(\mathrm{2}−\mathrm{n}\right)}{\mathrm{27}\left(\mathrm{25}+\mathrm{2n}^{\mathrm{2}} \right)}\left(\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}^{\mathrm{2}} +\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} \right)+\mathrm{20n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{4}\right)\geqslant\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{last}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{since}\:\mathrm{n}\leqslant\mathrm{2}\:\mathrm{hence}\:\mathrm{proven} \\ $$
Commented by Shrinava last updated on 04/Jul/22

$$\mathrm{a}\:=\:\mathrm{b}\:=\:\mathrm{c}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\: \\ $$
