
Question Number 172360 by Mikenice last updated on 25/Jun/22

Commented by mr W last updated on 25/Jun/22
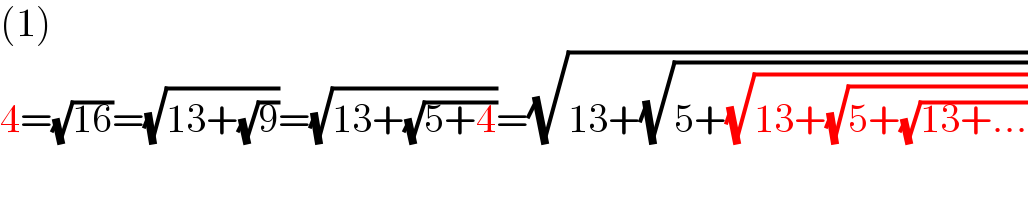
$$\left(\mathrm{1}\right) \\ $$$$\mathrm{4}=\sqrt{\mathrm{16}}=\sqrt{\mathrm{13}+\sqrt{\mathrm{9}}}=\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\mathrm{4}}}=\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+...}}}}} \\ $$
Commented by mr W last updated on 25/Jun/22

$$\left(\mathrm{2}\right) \\ $$$${see}\:{Q}#\:\mathrm{170948} \\ $$
Answered by Rasheed.Sindhi last updated on 26/Jun/22

$${Let}\:{x}=\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+...}}}}} \\ $$$${x}^{\mathrm{2}} −\mathrm{13}=\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+...}}}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{13}\right)^{\mathrm{2}} =\mathrm{5}+\sqrt{\mathrm{13}+\sqrt{\mathrm{5}+\sqrt{\mathrm{13}+...}}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{13}\right)^{\mathrm{2}} −\mathrm{5}={x} \\ $$$${See}\:{below}\:{the}\:{comments}\:{of}\:{mrW}\:\boldsymbol{{sir}}\downarrow \\ $$
Commented by mr W last updated on 25/Jun/22
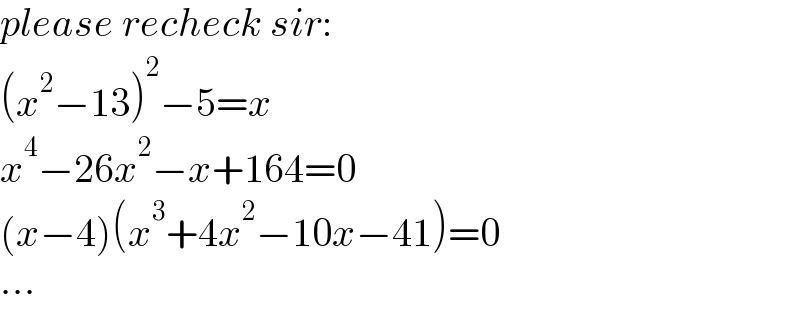
$${please}\:{recheck}\:{sir}: \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{13}\right)^{\mathrm{2}} −\mathrm{5}={x} \\ $$$${x}^{\mathrm{4}} −\mathrm{26}{x}^{\mathrm{2}} −{x}+\mathrm{164}=\mathrm{0} \\ $$$$\left({x}−\mathrm{4}\right)\left({x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{41}\right)=\mathrm{0} \\ $$$$... \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jun/22

$${You}'{re}\:{right}\:\boldsymbol{{sir}}! \\ $$
Commented by mr W last updated on 25/Jun/22
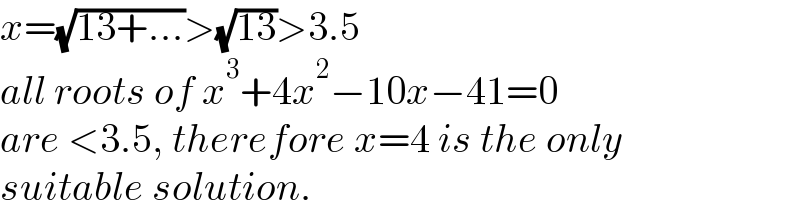
$${x}=\sqrt{\mathrm{13}+...}>\sqrt{\mathrm{13}}>\mathrm{3}.\mathrm{5} \\ $$$${all}\:{roots}\:{of}\:{x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{41}=\mathrm{0}\: \\ $$$${are}\:<\mathrm{3}.\mathrm{5},\:{therefore}\:{x}=\mathrm{4}\:{is}\:{the}\:{only} \\ $$$${suitable}\:{solution}. \\ $$
