
Question Number 171972 by mathlove last updated on 22/Jun/22
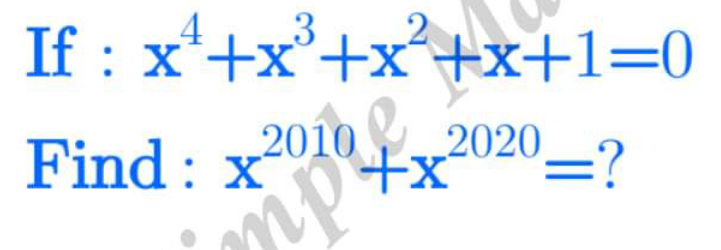
Answered by mr W last updated on 22/Jun/22
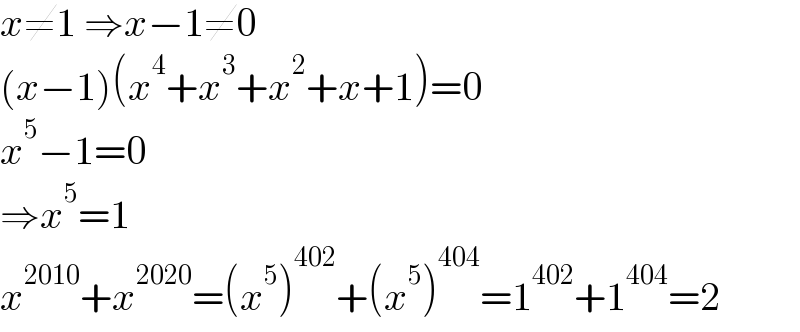
$${x}\neq\mathrm{1}\:\Rightarrow{x}−\mathrm{1}\neq\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{5}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{1} \\ $$$${x}^{\mathrm{2010}} +{x}^{\mathrm{2020}} =\left({x}^{\mathrm{5}} \right)^{\mathrm{402}} +\left({x}^{\mathrm{5}} \right)^{\mathrm{404}} =\mathrm{1}^{\mathrm{402}} +\mathrm{1}^{\mathrm{404}} =\mathrm{2} \\ $$
Commented by mathlove last updated on 22/Jun/22

$${thanks} \\ $$
Commented by infinityaction last updated on 22/Jun/22
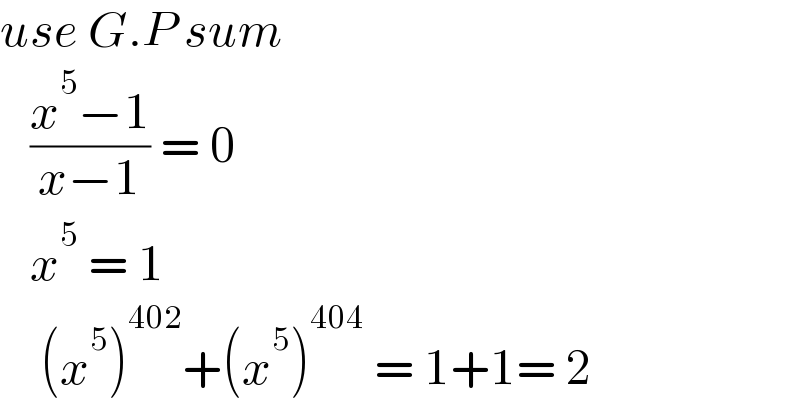
$${use}\:{G}.{P}\:{sum} \\ $$$$\:\:\:\frac{{x}^{\mathrm{5}} −\mathrm{1}}{{x}−\mathrm{1}}\:=\:\mathrm{0} \\ $$$$\:\:\:{x}^{\mathrm{5}} \:=\:\mathrm{1} \\ $$$$\:\:\:\:\left({x}^{\mathrm{5}} \right)^{\mathrm{402}} +\left({x}^{\mathrm{5}} \right)^{\mathrm{404}} \:=\:\mathrm{1}+\mathrm{1}=\:\mathrm{2} \\ $$
