Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 171253 by vonem1 last updated on 11/Jun/22

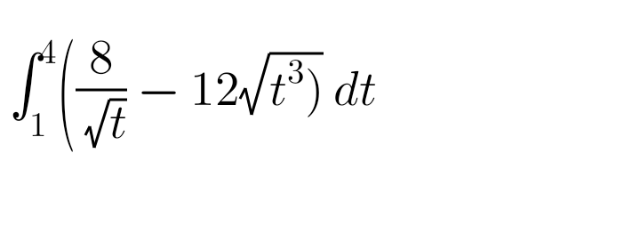
Answered by haladu last updated on 11/Jun/22

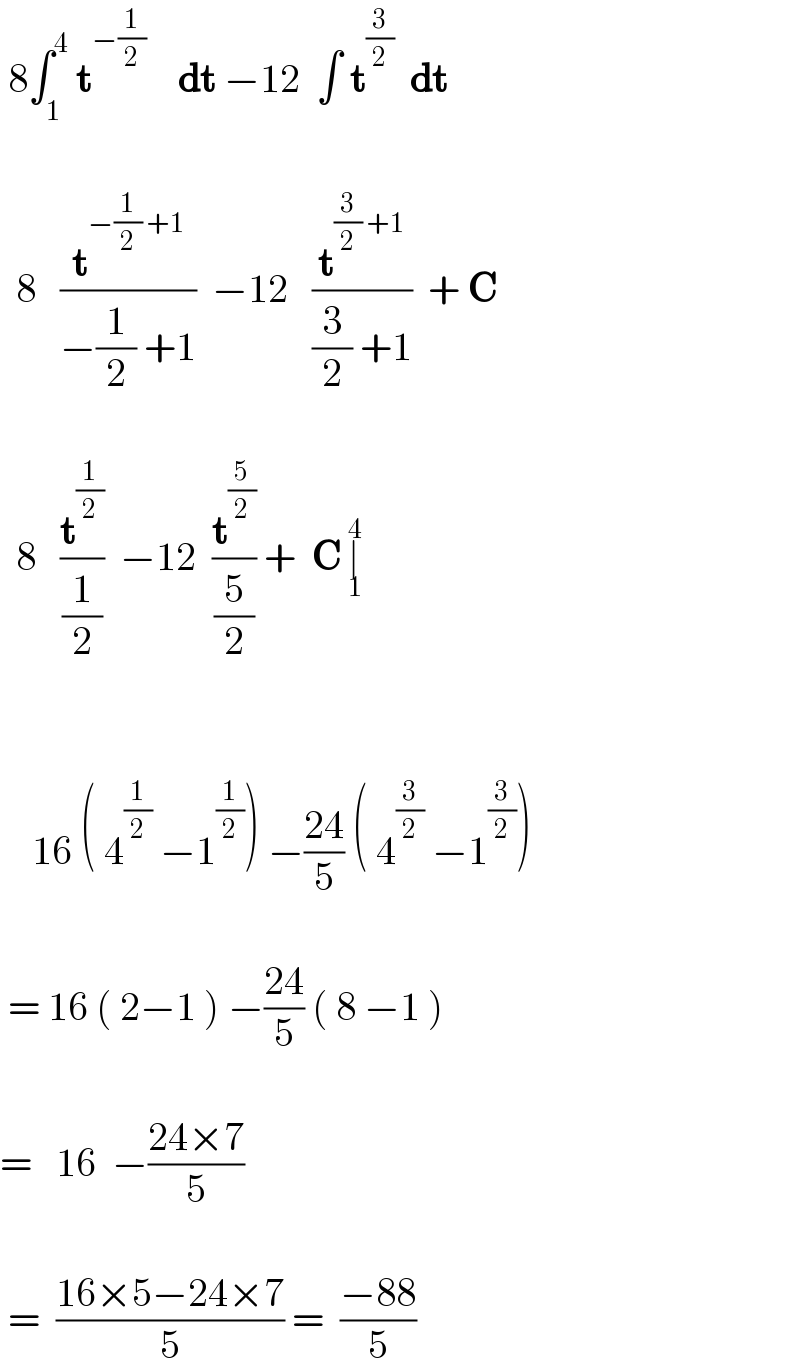
8∫_1 ^4 t^(−(1/2)) dt −12 ∫ t^(3/2) dt 8 (t^(−(1/2) +1) /(−(1/2) +1)) −12 (t^((3/2) +1) /((3/2) +1)) + C 8 (t^(1/2) /(1/2)) −12 (t^(5/2) /(5/2)) + C ∣_1 ^4 16 ( 4^(1/2) −1^(1/2) ) −((24)/5) ( 4^(3/2) −1^(3/2) ) = 16 ( 2−1 ) −((24)/5) ( 8 −1 ) = 16 −((24×7)/5) = ((16×5−24×7)/5) = ((−88)/5)

$$\:\mathrm{8}\int_{\mathrm{1}} ^{\mathrm{4}} \:\boldsymbol{\mathrm{t}}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\:\boldsymbol{\mathrm{dt}}\:−\mathrm{12}\:\:\int\:\boldsymbol{\mathrm{t}}^{\frac{\mathrm{3}}{\mathrm{2}}} \:\:\boldsymbol{\mathrm{dt}} \\ $$$$\:\:\: \\ $$$$\:\:\mathrm{8}\:\:\:\frac{\boldsymbol{\mathrm{t}}^{−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{1}} }{−\frac{\mathrm{1}}{\mathrm{2}}\:+\mathrm{1}}\:\:−\mathrm{12}\:\:\:\frac{\boldsymbol{\mathrm{t}}^{\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{1}} }{\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{1}}\:\:+\:\boldsymbol{\mathrm{C}} \\ $$$$\:\:\: \\ $$$$\:\:\mathrm{8}\:\:\:\frac{\boldsymbol{\mathrm{t}}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\frac{\mathrm{1}}{\mathrm{2}}}\:\:−\mathrm{12}\:\:\frac{\boldsymbol{\mathrm{t}}^{\frac{\mathrm{5}}{\mathrm{2}}} }{\frac{\mathrm{5}}{\mathrm{2}}}\:+\:\:\boldsymbol{\mathrm{C}}\:\underset{\mathrm{1}} {\overset{\mathrm{4}} {\mid}} \\ $$$$\:\: \\ $$$$\:\:\: \\ $$$$\:\:\:\:\mathrm{16}\:\left(\:\mathrm{4}^{\frac{\mathrm{1}}{\mathrm{2}}} \:−\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)\:−\frac{\mathrm{24}}{\mathrm{5}}\:\left(\:\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\mathrm{1}^{\frac{\mathrm{3}}{\mathrm{2}}} \right) \\ $$$$\:\: \\ $$$$\:=\:\mathrm{16}\:\left(\:\mathrm{2}−\mathrm{1}\:\right)\:−\frac{\mathrm{24}}{\mathrm{5}}\:\left(\:\mathrm{8}\:−\mathrm{1}\:\right) \\ $$$$\:\: \\ $$$$=\:\:\:\mathrm{16}\:\:−\frac{\mathrm{24}×\mathrm{7}}{\mathrm{5}} \\ $$$$\:\: \\ $$$$\:=\:\:\frac{\mathrm{16}×\mathrm{5}−\mathrm{24}×\mathrm{7}}{\mathrm{5}}\:=\:\:\frac{−\mathrm{88}}{\mathrm{5}} \\ $$

Answered by thfchristopher last updated on 11/Jun/22

=∫_1 ^4 (8t^(−(1/2)) −12t^(3/2) )dt =[16t^(1/2) −((24)/5)t^(5/2) ]_1 ^4 =32−((768)/5)−16+((24)/5) =−((664)/5)

$$=\int_{\mathrm{1}} ^{\mathrm{4}} \left(\mathrm{8}{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{12}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right){dt} \\ $$$$=\left[\mathrm{16}{t}^{\frac{\mathrm{1}}{\mathrm{2}}} −\frac{\mathrm{24}}{\mathrm{5}}{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \right]_{\mathrm{1}} ^{\mathrm{4}} \\ $$$$=\mathrm{32}−\frac{\mathrm{768}}{\mathrm{5}}−\mathrm{16}+\frac{\mathrm{24}}{\mathrm{5}} \\ $$$$=−\frac{\mathrm{664}}{\mathrm{5}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com