
Question Number 168161 by daus last updated on 05/Apr/22
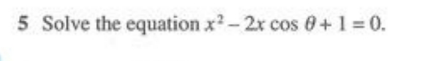
Commented by daus last updated on 05/Apr/22
$${help}\:{show}\:{me}\:{the}\:{way}.\:{thanks} \\ $$
Answered by alephzero last updated on 05/Apr/22
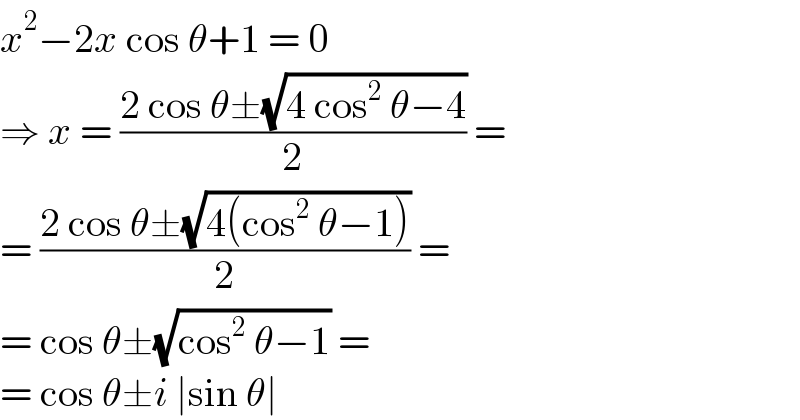
$${x}^{\mathrm{2}} −\mathrm{2}{x}\:\mathrm{cos}\:\theta+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}\:=\:\frac{\mathrm{2}\:\mathrm{cos}\:\theta\pm\sqrt{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{4}}}{\mathrm{2}}\:= \\ $$$$=\:\frac{\mathrm{2}\:\mathrm{cos}\:\theta\pm\sqrt{\mathrm{4}\left(\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}\right)}}{\mathrm{2}}\:= \\ $$$$=\:\mathrm{cos}\:\theta\pm\sqrt{\mathrm{cos}^{\mathrm{2}} \:\theta−\mathrm{1}}\:= \\ $$$$=\:\mathrm{cos}\:\theta\pm{i}\:\mid\mathrm{sin}\:\theta\mid \\ $$
Commented by peter frank last updated on 05/Apr/22

$$\mathrm{good} \\ $$
