
Question Number 168086 by mokys last updated on 02/Apr/22

Answered by som(math1967) last updated on 03/Apr/22
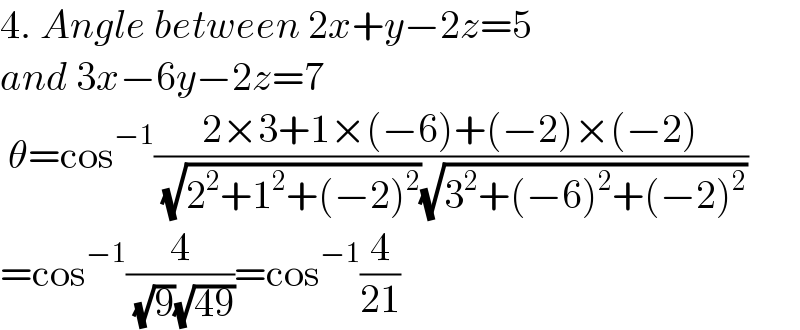
$$\mathrm{4}.\:{Angle}\:{between}\:\mathrm{2}{x}+{y}−\mathrm{2}{z}=\mathrm{5} \\ $$$${and}\:\mathrm{3}{x}−\mathrm{6}{y}−\mathrm{2}{z}=\mathrm{7} \\ $$$$\:\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{2}×\mathrm{3}+\mathrm{1}×\left(−\mathrm{6}\right)+\left(−\mathrm{2}\right)×\left(−\mathrm{2}\right)}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} }\sqrt{\mathrm{3}^{\mathrm{2}} +\left(−\mathrm{6}\right)^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} }} \\ $$$$=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\:\sqrt{\mathrm{9}}\sqrt{\mathrm{49}}}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{4}}{\mathrm{21}} \\ $$
