Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 167899 by peter frank last updated on 28/Mar/22

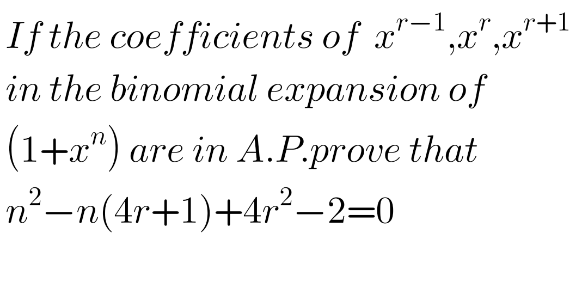
Answered by floor(10²Eta[1]) last updated on 29/Mar/22

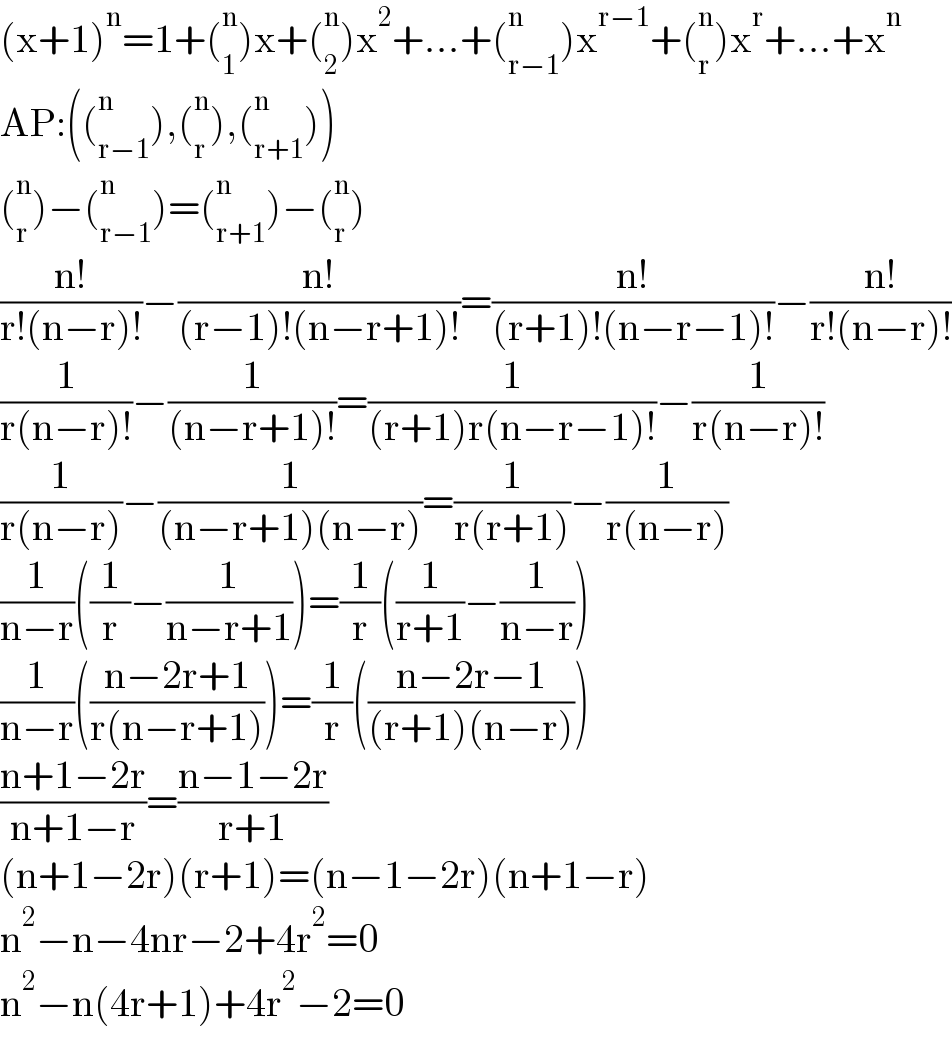
(x+1)^n =1+(_1 ^n )x+(_2 ^n )x^2 +...+(_(r−1) ^n )x^(r−1) +(_r ^n )x^r +...+x^n AP:((_(r−1) ^n ),(_r ^n ),(_(r+1) ^n )) (_r ^n )−(_(r−1) ^n )=(_(r+1) ^n )−(_r ^n ) ((n!)/(r!(n−r)!))−((n!)/((r−1)!(n−r+1)!))=((n!)/((r+1)!(n−r−1)!))−((n!)/(r!(n−r)!)) (1/(r(n−r)!))−(1/((n−r+1)!))=(1/((r+1)r(n−r−1)!))−(1/(r(n−r)!)) (1/(r(n−r)))−(1/((n−r+1)(n−r)))=(1/(r(r+1)))−(1/(r(n−r))) (1/(n−r))((1/r)−(1/(n−r+1)))=(1/r)((1/(r+1))−(1/(n−r))) (1/(n−r))(((n−2r+1)/(r(n−r+1))))=(1/r)(((n−2r−1)/((r+1)(n−r)))) ((n+1−2r)/(n+1−r))=((n−1−2r)/(r+1)) (n+1−2r)(r+1)=(n−1−2r)(n+1−r) n^2 −n−4nr−2+4r^2 =0 n^2 −n(4r+1)+4r^2 −2=0

$$\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{n}} =\mathrm{1}+\left(_{\mathrm{1}} ^{\mathrm{n}} \right)\mathrm{x}+\left(_{\mathrm{2}} ^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{2}} +...+\left(_{\mathrm{r}−\mathrm{1}} ^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{r}−\mathrm{1}} +\left(_{\mathrm{r}} ^{\mathrm{n}} \right)\mathrm{x}^{\mathrm{r}} +...+\mathrm{x}^{\mathrm{n}} \\ $$$$\mathrm{AP}:\left(\left(_{\mathrm{r}−\mathrm{1}} ^{\mathrm{n}} \right),\left(_{\mathrm{r}} ^{\mathrm{n}} \right),\left(_{\mathrm{r}+\mathrm{1}} ^{\mathrm{n}} \right)\right) \\ $$$$\left(_{\mathrm{r}} ^{\mathrm{n}} \right)−\left(_{\mathrm{r}−\mathrm{1}} ^{\mathrm{n}} \right)=\left(_{\mathrm{r}+\mathrm{1}} ^{\mathrm{n}} \right)−\left(_{\mathrm{r}} ^{\mathrm{n}} \right) \\ $$$$\frac{\mathrm{n}!}{\mathrm{r}!\left(\mathrm{n}−\mathrm{r}\right)!}−\frac{\mathrm{n}!}{\left(\mathrm{r}−\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)!}=\frac{\mathrm{n}!}{\left(\mathrm{r}+\mathrm{1}\right)!\left(\mathrm{n}−\mathrm{r}−\mathrm{1}\right)!}−\frac{\mathrm{n}!}{\mathrm{r}!\left(\mathrm{n}−\mathrm{r}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{r}\left(\mathrm{n}−\mathrm{r}\right)!}−\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{\left(\mathrm{r}+\mathrm{1}\right)\mathrm{r}\left(\mathrm{n}−\mathrm{r}−\mathrm{1}\right)!}−\frac{\mathrm{1}}{\mathrm{r}\left(\mathrm{n}−\mathrm{r}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{r}\left(\mathrm{n}−\mathrm{r}\right)}−\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)\left(\mathrm{n}−\mathrm{r}\right)}=\frac{\mathrm{1}}{\mathrm{r}\left(\mathrm{r}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{r}\left(\mathrm{n}−\mathrm{r}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}−\mathrm{r}}\left(\frac{\mathrm{1}}{\mathrm{r}}−\frac{\mathrm{1}}{\mathrm{n}−\mathrm{r}+\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{r}}\left(\frac{\mathrm{1}}{\mathrm{r}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}−\mathrm{r}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{n}−\mathrm{r}}\left(\frac{\mathrm{n}−\mathrm{2r}+\mathrm{1}}{\mathrm{r}\left(\mathrm{n}−\mathrm{r}+\mathrm{1}\right)}\right)=\frac{\mathrm{1}}{\mathrm{r}}\left(\frac{\mathrm{n}−\mathrm{2r}−\mathrm{1}}{\left(\mathrm{r}+\mathrm{1}\right)\left(\mathrm{n}−\mathrm{r}\right)}\right) \\ $$$$\frac{\mathrm{n}+\mathrm{1}−\mathrm{2r}}{\mathrm{n}+\mathrm{1}−\mathrm{r}}=\frac{\mathrm{n}−\mathrm{1}−\mathrm{2r}}{\mathrm{r}+\mathrm{1}} \\ $$$$\left(\mathrm{n}+\mathrm{1}−\mathrm{2r}\right)\left(\mathrm{r}+\mathrm{1}\right)=\left(\mathrm{n}−\mathrm{1}−\mathrm{2r}\right)\left(\mathrm{n}+\mathrm{1}−\mathrm{r}\right) \\ $$$$\mathrm{n}^{\mathrm{2}} −\mathrm{n}−\mathrm{4nr}−\mathrm{2}+\mathrm{4r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{n}^{\mathrm{2}} −\mathrm{n}\left(\mathrm{4r}+\mathrm{1}\right)+\mathrm{4r}^{\mathrm{2}} −\mathrm{2}=\mathrm{0} \\ $$

Commented by peter frank last updated on 29/Mar/22

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com