
Question Number 16785 by RasheedSoomro last updated on 26/Jun/17
Commented by RasheedSoomro last updated on 26/Jun/17

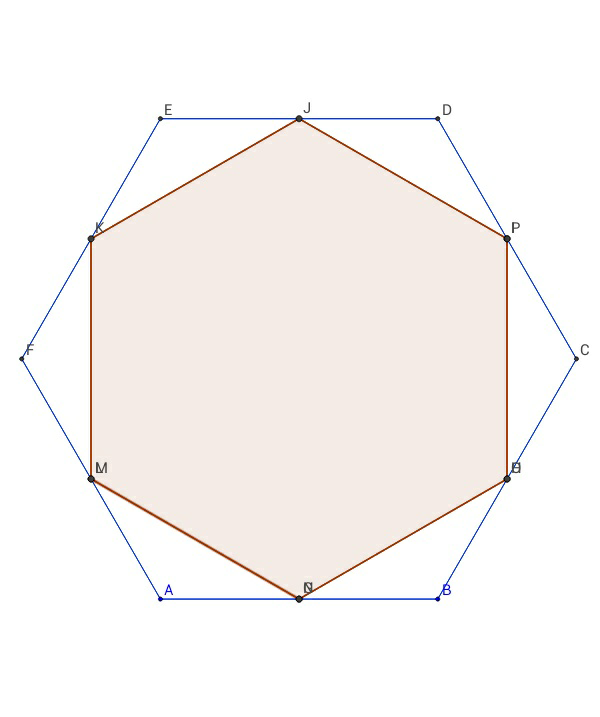
$$\mathrm{Without}\:\mathrm{using}\:\mathrm{area}-\mathrm{formula}\:\mathrm{find}\:\mathrm{out} \\ $$$$\mathrm{the}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part}\:\mathrm{to}\:\mathrm{the}\:\mathrm{whole}. \\ $$
Commented by mrW1 last updated on 26/Jun/17

$$\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Answered by sandy_suhendra last updated on 27/Jun/17
$$\mathrm{AB}=\mathrm{BC}=\mathrm{CD}=\mathrm{DE}=\mathrm{EF}=\mathrm{FA}=\mathrm{x} \\ $$$$\mathrm{JK}=\mathrm{KM}=\mathrm{MN}=\mathrm{NS}=\mathrm{SP}=\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\right)^{\mathrm{2}} \mathrm{cos}\:\mathrm{120}°}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\sqrt{\mathrm{3}}\:\:\:\:\: \\ $$$$\mathrm{A}_{\mathrm{JKMNSP}} \::\:\mathrm{A}_{\mathrm{ABCDEF}} \:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} :\:\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by RasheedSoomro last updated on 28/Jun/17

$$\mathcal{T}{hanks}\:\mathcal{SANDY}! \\ $$
Answered by RasheedSoomro last updated on 28/Jun/17
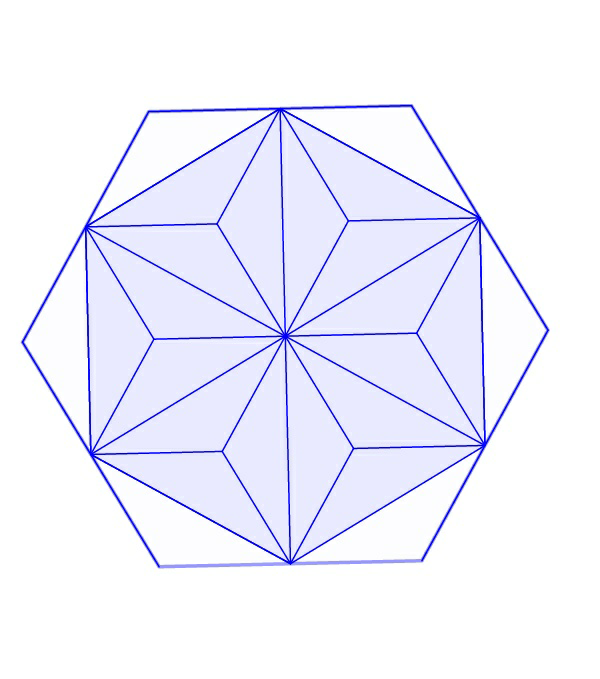
Commented by RasheedSoomro last updated on 28/Jun/17

$$\mathrm{Ratio}\:\mathrm{of}\:\mathrm{shaded}\:\mathrm{part}\:\mathrm{to}\:\mathrm{whole} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{small}\:\mathrm{triangles}\:\mathrm{in}\:\mathrm{shaded}\:\mathrm{part}}{\mathrm{small}\:\mathrm{triangles}\:\mathrm{in}\:\mathrm{whole}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{18}}{\mathrm{24}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Commented by mrW1 last updated on 28/Jun/17

$$\mathrm{very}\:\mathrm{fine}! \\ $$
