Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 167795 by niverland last updated on 25/Mar/22

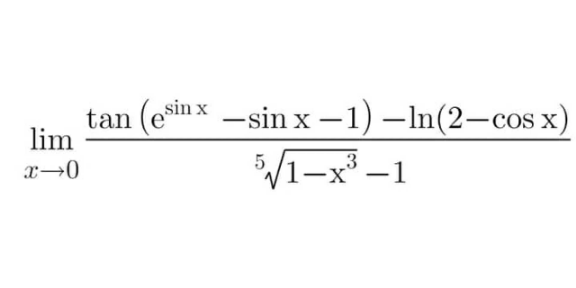
Commented by MJS_new last updated on 25/Mar/22

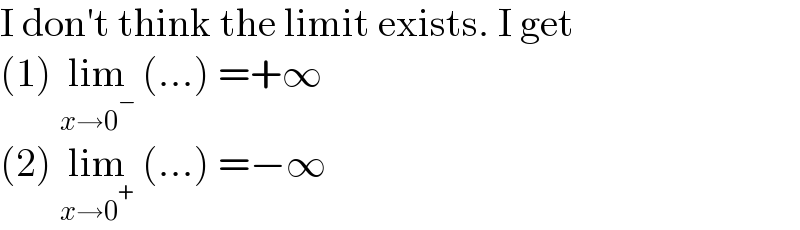
I don′t think the limit exists. I get (1) lim_(x→0^− ) (...) =+∞ (2) lim_(x→0^+ ) (...) =−∞

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{exists}.\:\mathrm{I}\:\mathrm{get} \\ $$$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\:\left(...\right)\:=+\infty \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(...\right)\:=−\infty \\ $$

Answered by qaz last updated on 25/Mar/22

lim_(x→0) ((tan (e^(sin x) −sin −1)−ln(2−cos x))/( ((1−x^3 ))^(1/5) −1)) =lim_(x→0) ((sec^2 (e^(sin x) −sin x−1)∙(e^(sin x) cos x−cos x)−((sin x)/(2−cos x)))/((−(1/5)x^3 )′)) =lim_(x→0) (((2−cos x)∙cos x∙sec^2 (e^(sin x) −sin x−1)∙(e^(sin x) −1)−sin x)/(−(3/5)x^2 (2−cos x))) =lim_(x→0) (((2−cos x)∙cos x∙sec^2 (e^(sin x) −sin x−1)∙(sin x+(1/2)sin^2 x+o(sin^2 x))−sin x)/(−(3/5)x^2 (2−cos x))) =lim_(x→0) (((2−cos x)∙cos x∙sec^2 (e^(sin x) −sin x−1)∙(1+(1/2)sin x+o(sin x))−1)/(−(3/5)x(2−cos x))) =lim_(x→0) ((ln[(2−cos x)∙cos x∙sec^2 (e^(sin x) −sin x−1)∙(1+(1/2)sin x+o(sin x))])/(−(3/5)x(2−cos x))) =lim_(x→0) ((ln(1+(1/2)sin x+o(sin x)))/(−(3/5)x(2−cos x))) =lim_(x→0) (((1/2)sin x+o(sin x))/(−(3/5)x(2−cos x))) =−(5/6) −−−−−−−−−−− lim_(x→0) ((ln(sec^2 (e^(sin x) −sin x−1)))/(−(3/5)x(2−cos x)))=lim_(x→0) ((−2ln(cos (e^(sin x) −sin x−1)))/(−(3/5)x(2−cos x))) =lim_(x→0) ((−2(cos ((1/2)sin^2 x+o(sin^2 x))−1))/(−(3/5)x(2−cos x))) =lim_(x→0) ((−2(−(1/8)sin^4 x+o(sin^4 x)))/(−(3/5)x(2−cos x)))=0

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:−\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)}{\:\sqrt[{\mathrm{5}}]{\mathrm{1}−\mathrm{x}^{\mathrm{3}} }−\mathrm{1}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\centerdot\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} \mathrm{cos}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{2}−\mathrm{cos}\:\mathrm{x}}}{\left(−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} \right)'} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)\centerdot\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\centerdot\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{1}\right)−\mathrm{sin}\:\mathrm{x}}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)\centerdot\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\centerdot\left(\mathrm{sin}\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{o}\left(\mathrm{sin}^{\mathrm{2}} \:\mathrm{x}\right)\right)−\mathrm{sin}\:\mathrm{x}}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)\centerdot\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\centerdot\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:\mathrm{x}\right)\right)−\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left[\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)\centerdot\mathrm{cos}\:\mathrm{x}\centerdot\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\centerdot\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:\mathrm{x}\right)\right)\right]}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:\mathrm{x}\right)\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:\mathrm{x}\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=−\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$−−−−−−−−−−− \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{ln}\left(\mathrm{sec}\:^{\mathrm{2}} \left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)}=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2ln}\left(\mathrm{cos}\:\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\left(\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)\right)−\mathrm{1}\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2}\left(−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}+\mathrm{o}\left(\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\right)\right)}{−\frac{\mathrm{3}}{\mathrm{5}}\mathrm{x}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)}=\mathrm{0} \\ $$

Commented by MJS_new last updated on 25/Mar/22

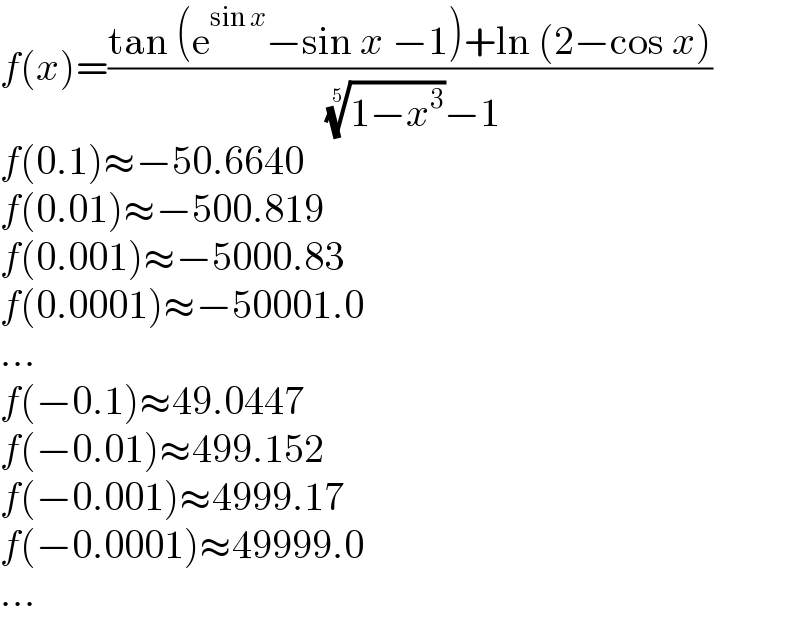
f(x)=((tan (e^(sin x) −sin x −1)+ln (2−cos x))/( ((1−x^3 ))^(1/5) −1)) f(0.1)≈−50.6640 f(0.01)≈−500.819 f(0.001)≈−5000.83 f(0.0001)≈−50001.0 ... f(−0.1)≈49.0447 f(−0.01)≈499.152 f(−0.001)≈4999.17 f(−0.0001)≈49999.0 ...

$${f}\left({x}\right)=\frac{\mathrm{tan}\:\left(\mathrm{e}^{\mathrm{sin}\:{x}} −\mathrm{sin}\:{x}\:−\mathrm{1}\right)+\mathrm{ln}\:\left(\mathrm{2}−\mathrm{cos}\:{x}\right)}{\:\sqrt[{\mathrm{5}}]{\mathrm{1}−{x}^{\mathrm{3}} }−\mathrm{1}} \\ $$$${f}\left(\mathrm{0}.\mathrm{1}\right)\approx−\mathrm{50}.\mathrm{6640} \\ $$$${f}\left(\mathrm{0}.\mathrm{01}\right)\approx−\mathrm{500}.\mathrm{819} \\ $$$${f}\left(\mathrm{0}.\mathrm{001}\right)\approx−\mathrm{5000}.\mathrm{83} \\ $$$${f}\left(\mathrm{0}.\mathrm{0001}\right)\approx−\mathrm{50001}.\mathrm{0} \\ $$$$... \\ $$$${f}\left(−\mathrm{0}.\mathrm{1}\right)\approx\mathrm{49}.\mathrm{0447} \\ $$$${f}\left(−\mathrm{0}.\mathrm{01}\right)\approx\mathrm{499}.\mathrm{152} \\ $$$${f}\left(−\mathrm{0}.\mathrm{001}\right)\approx\mathrm{4999}.\mathrm{17} \\ $$$${f}\left(−\mathrm{0}.\mathrm{0001}\right)\approx\mathrm{49999}.\mathrm{0} \\ $$$$... \\ $$

Answered by qaz last updated on 25/Mar/22

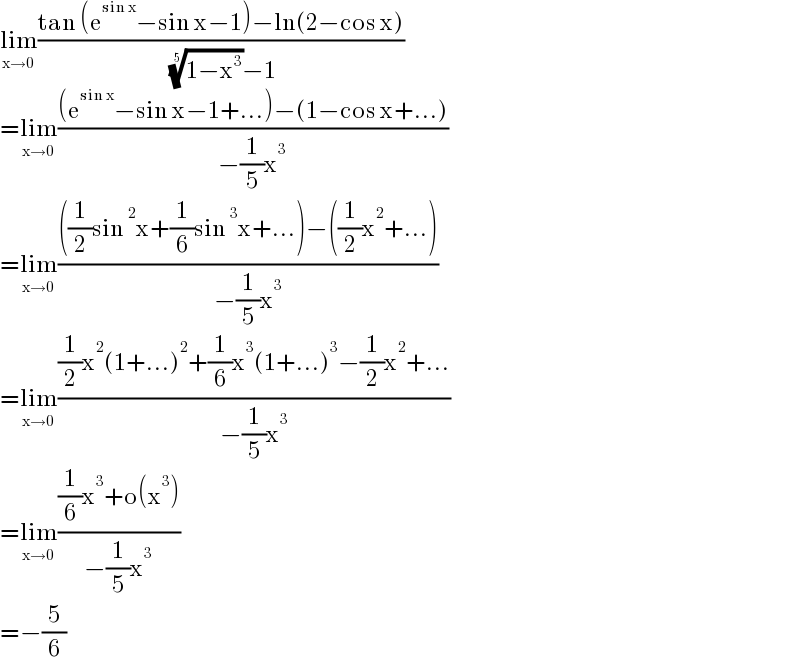
lim_(x→0) ((tan (e^(sin x) −sin x−1)−ln(2−cos x))/( ((1−x^3 ))^(1/5) −1)) =lim_(x→0) (((e^(sin x) −sin x−1+...)−(1−cos x+...))/(−(1/5)x^3 )) =lim_(x→0) ((((1/2)sin^2 x+(1/6)sin^3 x+...)−((1/2)x^2 +...))/(−(1/5)x^3 )) =lim_(x→0) (((1/2)x^2 (1+...)^2 +(1/6)x^3 (1+...)^3 −(1/2)x^2 +...)/(−(1/5)x^3 )) =lim_(x→0) (((1/6)x^3 +o(x^3 ))/(−(1/5)x^3 )) =−(5/6)

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{tan}\:\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{2}−\mathrm{cos}\:\mathrm{x}\right)}{\:\sqrt[{\mathrm{5}}]{\mathrm{1}−\mathrm{x}^{\mathrm{3}} }−\mathrm{1}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{e}^{\mathrm{sin}\:\mathrm{x}} −\mathrm{sin}\:\mathrm{x}−\mathrm{1}+...\right)−\left(\mathrm{1}−\mathrm{cos}\:\mathrm{x}+...\right)}{−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+...\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +...\right)}{−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{1}+...\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \left(\mathrm{1}+...\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} +...}{−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)}{−\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{3}} } \\ $$$$=−\frac{\mathrm{5}}{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com