Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 167699 by HongKing last updated on 23/Mar/22

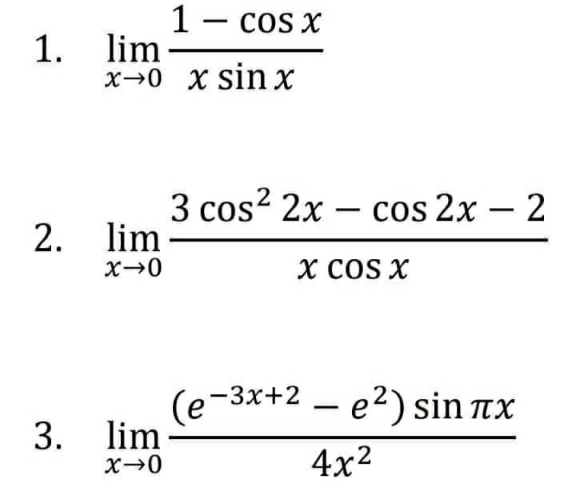
Answered by alephzero last updated on 23/Mar/22

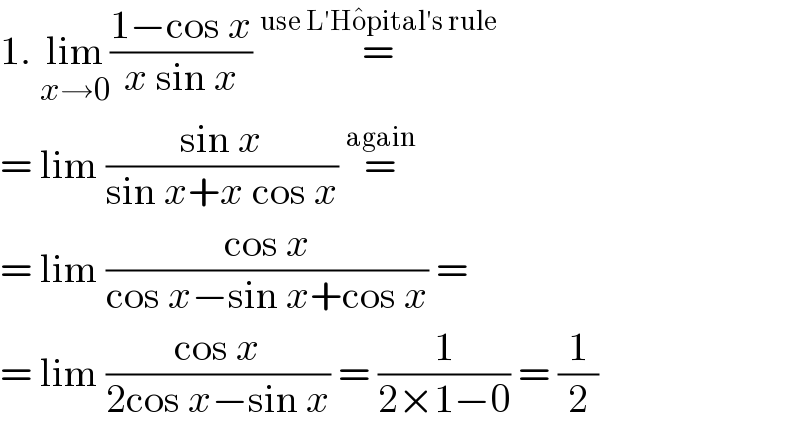
1. lim_(x→0) ((1−cos x)/(x sin x)) =^(use L′Ho^� pital′s rule) = lim ((sin x)/(sin x+x cos x)) =^(again) = lim ((cos x)/(cos x−sin x+cos x)) = = lim ((cos x)/(2cos x−sin x)) = (1/(2×1−0)) = (1/2)

$$\mathrm{1}.\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:{x}}{{x}\:\mathrm{sin}\:{x}}\:\overset{\mathrm{use}\:\mathrm{L}'\mathrm{H}\hat {\mathrm{o}pital}'\mathrm{s}\:\mathrm{rule}} {=} \\ $$$$=\:\mathrm{lim}\:\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}+{x}\:\mathrm{cos}\:{x}}\:\overset{\mathrm{again}} {=} \\ $$$$=\:\mathrm{lim}\:\frac{\mathrm{cos}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}\:= \\ $$$$=\:\mathrm{lim}\:\frac{\mathrm{cos}\:{x}}{\mathrm{2cos}\:{x}−\mathrm{sin}\:{x}}\:=\:\frac{\mathrm{1}}{\mathrm{2}×\mathrm{1}−\mathrm{0}}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by alephzero last updated on 23/Mar/22

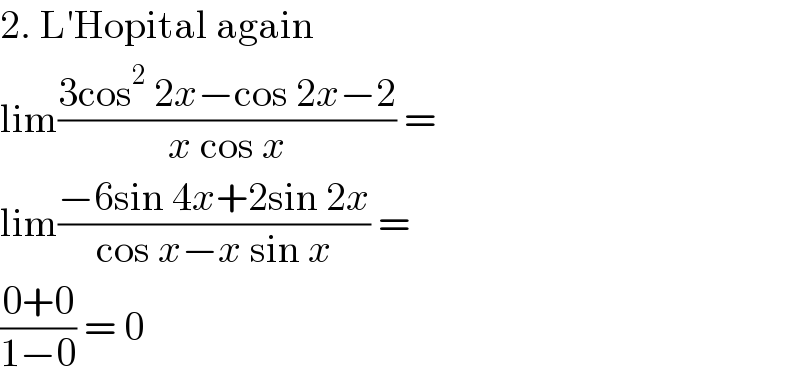
2. L′Hopital again lim((3cos^2 2x−cos 2x−2)/(x cos x)) = lim((−6sin 4x+2sin 2x)/(cos x−x sin x)) = ((0+0)/(1−0)) = 0

$$\mathrm{2}.\:\mathrm{L}'\mathrm{Hopital}\:\mathrm{again} \\ $$$$\mathrm{lim}\frac{\mathrm{3cos}^{\mathrm{2}} \:\mathrm{2}{x}−\mathrm{cos}\:\mathrm{2}{x}−\mathrm{2}}{{x}\:\mathrm{cos}\:{x}}\:=\: \\ $$$$\mathrm{lim}\frac{−\mathrm{6sin}\:\mathrm{4}{x}+\mathrm{2sin}\:\mathrm{2}{x}}{\mathrm{cos}\:{x}−{x}\:\mathrm{sin}\:{x}}\:= \\ $$$$\frac{\mathrm{0}+\mathrm{0}}{\mathrm{1}−\mathrm{0}}\:=\:\mathrm{0} \\ $$

Answered by qaz last updated on 23/Mar/22

lim_(x→0) (((e^(−3x+2) −e^2 )sin πx)/(4x^2 )) =lim_(x→0) ((e^2 πx(e^(−3x) −1))/(4x^2 )) =lim_(x→0) ((πe^2 )/(4x))(−3x+o(x)) =−(3/4)πe^2

$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{e}^{−\mathrm{3x}+\mathrm{2}} −\mathrm{e}^{\mathrm{2}} \right)\mathrm{sin}\:\pi\mathrm{x}}{\mathrm{4x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{e}^{\mathrm{2}} \pi\mathrm{x}\left(\mathrm{e}^{−\mathrm{3x}} −\mathrm{1}\right)}{\mathrm{4x}^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\pi\mathrm{e}^{\mathrm{2}} }{\mathrm{4x}}\left(−\mathrm{3x}+\mathrm{o}\left(\mathrm{x}\right)\right) \\ $$$$=−\frac{\mathrm{3}}{\mathrm{4}}\pi\mathrm{e}^{\mathrm{2}} \\ $$

Answered by malwan last updated on 24/Mar/22

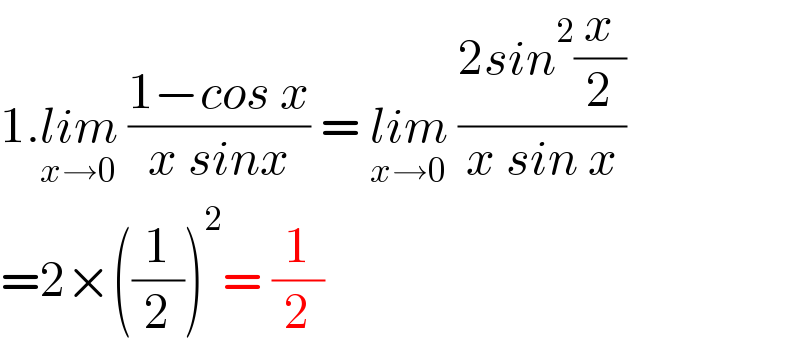
1.lim_(x→0) ((1−cos x)/(x sinx)) = lim_(x→0) ((2sin^2 (x/2))/(x sin x)) =2×((1/2))^2 = (1/2)

$$\mathrm{1}.\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mathrm{1}−{cos}\:{x}}{{x}\:{sinx}}\:=\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{{x}\:{sin}\:{x}} \\ $$$$=\mathrm{2}×\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com