
Question Number 167456 by Khalmohmmad last updated on 17/Mar/22
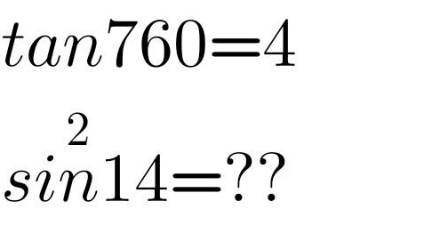
Answered by MJS_new last updated on 17/Mar/22

$$\mathrm{tan}\:\mathrm{760}\:\neq\mathrm{4} \\ $$$$\mathrm{tan}\:\mathrm{76}°\:\neq\mathrm{4} \\ $$$$\mathrm{sin}\:\mathrm{14}\:\approx.\mathrm{990607} \\ $$$$\mathrm{sin}\:\mathrm{14}°\:\approx.\mathrm{241922} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{14}\:\approx.\mathrm{981303} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{14}°\:\approx.\mathrm{0585262} \\ $$$$ \\ $$$$\mathrm{for}\:\alpha\:\mathrm{in}\:\mathrm{degree}: \\ $$$$\mathrm{tan}\:\alpha\:={t}\:\Rightarrow\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{90}−\alpha\right)\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{if}\:\mathrm{tan}\:\alpha\:=\mathrm{4}\:\Rightarrow\:\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{90}−\alpha\right)\:=\frac{\mathrm{1}}{\mathrm{17}} \\ $$
