
Question Number 167393 by DrHZ last updated on 15/Mar/22
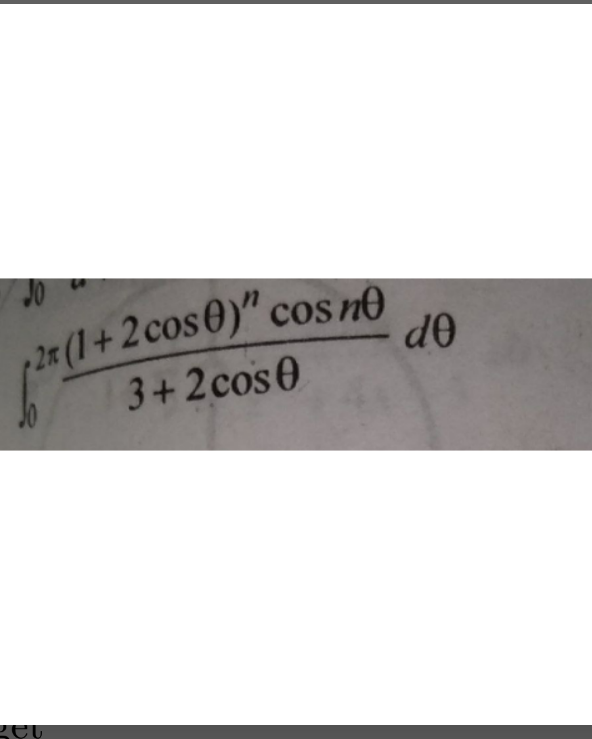
Answered by mindispower last updated on 15/Mar/22
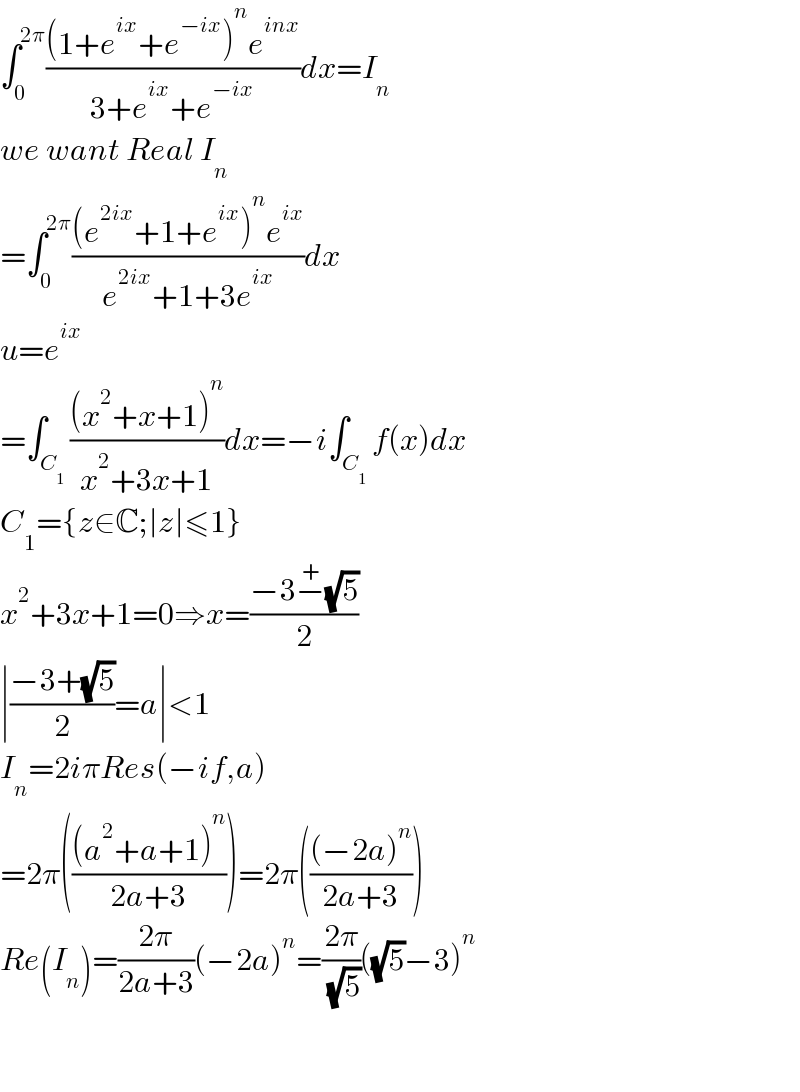
$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\left(\mathrm{1}+{e}^{{ix}} +{e}^{−{ix}} \right)^{{n}} {e}^{{inx}} }{\mathrm{3}+{e}^{{ix}} +{e}^{−{ix}} }{dx}={I}_{{n}} \\ $$$${we}\:{want}\:{Real}\:{I}_{{n}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{\left({e}^{\mathrm{2}{ix}} +\mathrm{1}+{e}^{{ix}} \right)^{{n}} {e}^{{ix}} }{{e}^{\mathrm{2}{ix}} +\mathrm{1}+\mathrm{3}{e}^{{ix}} }{dx} \\ $$$${u}={e}^{{ix}} \\ $$$$=\int_{{C}_{\mathrm{1}} } \frac{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)^{{n}} }{{x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}}{dx}=−{i}\int_{{C}_{\mathrm{1}} } {f}\left({x}\right){dx} \\ $$$${C}_{\mathrm{1}} =\left\{{z}\in\mathbb{C};\mid{z}\mid\leqslant\mathrm{1}\right\} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\frac{−\mathrm{3}\overset{+} {−}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\mid\frac{−\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}={a}\mid<\mathrm{1} \\ $$$${I}_{{n}} =\mathrm{2}{i}\pi{Res}\left(−{if},{a}\right) \\ $$$$=\mathrm{2}\pi\left(\frac{\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)^{{n}} }{\mathrm{2}{a}+\mathrm{3}}\right)=\mathrm{2}\pi\left(\frac{\left(−\mathrm{2}{a}\right)^{{n}} }{\mathrm{2}{a}+\mathrm{3}}\right) \\ $$$${Re}\left({I}_{{n}} \right)=\frac{\mathrm{2}\pi}{\mathrm{2}{a}+\mathrm{3}}\left(−\mathrm{2}{a}\right)^{{n}} =\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{5}}}\left(\sqrt{\mathrm{5}}−\mathrm{3}\right)^{{n}} \\ $$$$ \\ $$$$ \\ $$
