
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 167183 by alcohol last updated on 09/Mar/22

Commented by ArielVyny last updated on 09/Mar/22

$${i}\:{let}\:{question}\:\left({f}\right)\:{for}\:{your}\:{attention} \\ $$
Answered by ArielVyny last updated on 09/Mar/22

$$\left.{a}\right){showing}\:{that}\:\left({U}_{{n}} \right)\:{and}\:\left({V}_{{n}} \right)\:{are}\:{strictly} \\ $$$${positive}\:{sequences}. \\ $$$${reasonnig}\:{by}\:{reccurence}\:{on}\: \\ $$$${we}\:{have}\:{U}_{\mathrm{0}} =\mathrm{1}\:{and}\:{V}_{\mathrm{0}} =\mathrm{2}\:\:{also}\:{are}\:{strictly} \\ $$$${positive} \\ $$$${we}\:{suppose}\:{that}\:\left({U}_{{n}} \right)\:{ans}\:\left({V}_{{n}} \right)\:{are}\:{strictly}\: \\ $$$${positive}\:{then}\:{we}\:{have}\:{U}_{{n}} >\mathrm{0}\:\:{and}\:{V}_{{n}} >\mathrm{0} \\ $$$${now}\:{we}\:{will}\:{sbowing}\:{that}\:{U}_{{n}+\mathrm{1}} \:{and}\:{V}_{{n}+\mathrm{1}} \\ $$$${are}\:{strictly}\:{posirive} \\ $$$${V}_{{n}+\mathrm{1}} =\frac{{U}_{{n}} +{V}_{{n}} }{\mathrm{2}}\:\:{according}\:{that}\:{U}_{{n}} \:{and}\:{V}_{{n}} \:{are} \\ $$$${stritly}\:{positive}\:{and}\:\mathrm{2}>\mathrm{0}\:\left({evidence}\right)\:{we} \\ $$$${have}\:{V}_{{n}+\mathrm{1}} >\mathrm{0} \\ $$$${and}\:{U}_{{n}+\mathrm{1}} =\frac{{U}_{{n}} {V}_{{n}} }{{V}_{{n}+\mathrm{1}} }\:\:{we}\:{know}\:{that}\:{V}_{{n}+\mathrm{1}} >\mathrm{0} \\ $$$${and}\:{U}_{{n}} {V}_{{n}} \:{is}\:{strictly}\:{positive}\:{because}\:{it}'{s}\:{a} \\ $$$${product}\:{of}\:{two}\:{positives}\:{values} \\ $$$$ \\ $$
Answered by ArielVyny last updated on 09/Mar/22

$$\left({b}\right)\:{shosing}\:{that}\:\mathrm{0}\leqslant{W}_{{n}+\mathrm{1}} \leqslant\frac{\mathrm{1}}{\mathrm{2}}{W}_{{n}} \\ $$$${w}_{{n}} ={v}_{{n}} −{u}_{{n}} \rightarrow{w}_{{n}+\mathrm{1}} ={v}_{{n}+\mathrm{1}} −{u}_{{n}+\mathrm{1}} \\ $$$$\rightarrow{w}_{{n}+\mathrm{1}} =\frac{{u}_{{n}} +{v}_{{n}} }{\mathrm{2}}−\frac{\mathrm{2}{u}_{{n}} {v}_{{n}} }{{u}_{{n}} +{v}_{{n}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left({u}_{{n}} +{v}_{{n}} \right)^{\mathrm{2}} }{\mathrm{2}\left({u}_{{n}} +{v}_{{n}} \right)}−\frac{\mathrm{4}{u}_{{n}} {v}_{{n}} }{\mathrm{2}\left({u}_{{n}} +{v}_{{n}} \right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{u}_{{n}} ^{\mathrm{2}} +{v}_{{n}} ^{\mathrm{2}} −\mathrm{2}{u}_{{n}} {v}_{{n}} }{\mathrm{2}\left({u}_{{n}} +{v}_{{n}} \right)}=\frac{\left({u}_{{n}} −{v}_{{n}} \right)^{\mathrm{2}} }{\mathrm{2}\left({u}_{{n}} +{v}_{{n}} \right)}\geqslant\mathrm{0}\:\left({question}\:{a}\right) \\ $$$$\mathrm{0}\leqslant{w}_{{n}+\mathrm{1}} \\ $$$$\rightarrow{w}_{{n}+\mathrm{1}} −\frac{{w}_{{n}} }{\mathrm{2}}=\frac{{u}_{{n}} +{v}_{{n}} }{\mathrm{2}}−\frac{\mathrm{2}{u}_{{n}} {v}_{{n}} }{{u}_{{n}} +{v}_{{n}} }−\frac{{v}_{{n}} }{\mathrm{2}}+\frac{{u}_{{n}} }{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={u}_{{n}} −\frac{\mathrm{2}{u}_{{n}} {v}_{{n}} }{{u}_{{n}} +{v}_{{n}} }={u}_{{n}} \left(\mathrm{1}−\frac{\mathrm{2}{v}_{{n}} }{{u}_{{n}} +{v}_{{n}} }\right) \\ $$$${w}_{{n}+\mathrm{1}} \geqslant\mathrm{0}\rightarrow{w}_{{n}} \geqslant\mathrm{0}\:{and}\:{v}_{{n}} \geqslant{u}_{{n}} \\ $$$$\frac{\mathrm{2}{v}_{{n}} }{{u}_{{n}} +{v}_{{n}} }=\frac{{v}_{{n}} }{{v}_{{n}+\mathrm{1}} }\geqslant\frac{\mathrm{1}}{\mathrm{2}}\rightarrow\mathrm{2}{v}_{{n}} \geqslant{v}_{{n}+\mathrm{1}} \rightarrow\mathrm{2}{v}_{{n}} −\frac{{u}_{{n}} }{\mathrm{2}}−\frac{{v}_{{n}} }{\mathrm{2}}\geqslant\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\rightarrow\frac{\mathrm{3}}{\mathrm{2}}{v}_{{n}} −\frac{{u}_{{n}} }{\mathrm{2}}\geqslant\mathrm{0}\:\left({true}\right)\:{because}\:{v}_{{n}} >{u}_{{n}} \\ $$$${then}\:{we}\:{show}\:{that}\:\mathrm{1}−\frac{\mathrm{2}{v}_{{n}} }{{u}_{{n}} +{v}_{{n}} }\leqslant\mathrm{0}\:{then} \\ $$$${w}_{{n}+\mathrm{1}} −\frac{{w}_{{n}} }{\mathrm{2}}\leqslant\mathrm{0} \\ $$$${conclusion}\:\mathrm{0}\leqslant{w}_{{n}+\mathrm{1}} \leqslant\frac{{w}_{{n}} }{\mathrm{2}} \\ $$
Answered by ArielVyny last updated on 09/Mar/22

$$\left.{c}\right){show}\:{that}\:\mathrm{0}\leqslant{w}_{{n}+\mathrm{1}} \leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${by}\:{reccurence}\:{on}\:{n} \\ $$$$\mathrm{0}\leqslant{w}_{\mathrm{0}} \leqslant\mathrm{1}\:{with}\:{w}_{\mathrm{0}} =\mathrm{1} \\ $$$${suppose}\:{thant}\:\mathrm{0}\leqslant{w}_{{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} } \\ $$$${knowing}\:{that}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\geqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:{and}\:\:{w}_{{n}+\mathrm{1}} \leqslant\frac{{w}_{{n}} }{\mathrm{2}}\leqslant{w}_{{n}} \\ $$$$\mathrm{0}\leqslant{w}_{{n}} \leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\rightarrow\mathrm{0}\leqslant\frac{{w}_{{n}} }{\mathrm{2}}\leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\rightarrow\mathrm{0}\leqslant{w}_{{n}+\mathrm{1}} \leqslant\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${wd}\:{deduce}\:{that}\:{lim}\:{w}_{{n}+\mathrm{1}} =\mathrm{0}\:\left({by}\:{gendarm}'{s}\:{theorem}\right) \\ $$$${and}\:{lim}\:{w}_{{n}+\mathrm{1}} ={lim}\:{w}_{{n}} =\mathrm{0} \\ $$
Answered by ArielVyny last updated on 09/Mar/22
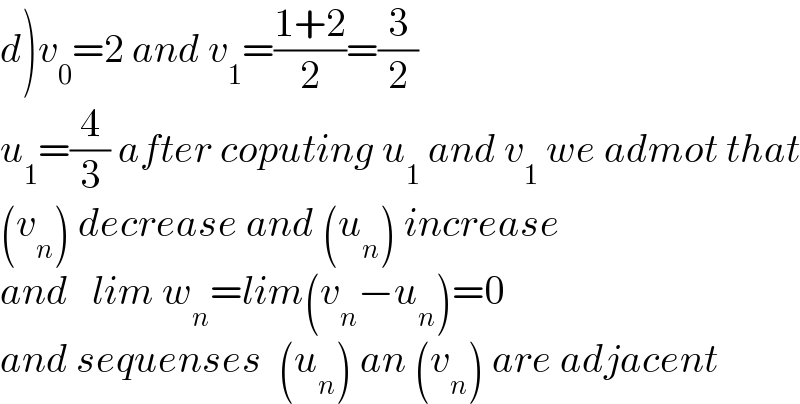
$$\left.{d}\right){v}_{\mathrm{0}} =\mathrm{2}\:{and}\:{v}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${u}_{\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{3}}\:{after}\:{coputing}\:{u}_{\mathrm{1}} \:{and}\:{v}_{\mathrm{1}} \:{we}\:{admot}\:{that} \\ $$$$\left({v}_{{n}} \right)\:{decrease}\:{and}\:\left({u}_{{n}} \right)\:{increase} \\ $$$${and}\:\:\:{lim}\:{w}_{{n}} ={lim}\left({v}_{{n}} −{u}_{{n}} \right)=\mathrm{0} \\ $$$${and}\:{sequenses}\:\:\left({u}_{{n}} \right)\:{an}\:\left({v}_{{n}} \right)\:{are}\:{adjacent} \\ $$
Answered by ArielVyny last updated on 09/Mar/22
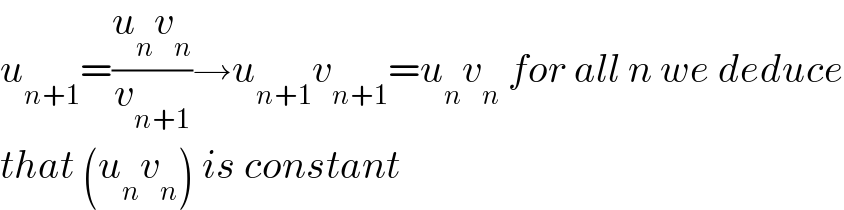
$${u}_{{n}+\mathrm{1}} =\frac{{u}_{{n}} {v}_{{n}} }{{v}_{{n}+\mathrm{1}} }\rightarrow{u}_{{n}+\mathrm{1}} {v}_{{n}+\mathrm{1}} ={u}_{{n}} {v}_{{n}} \:{for}\:{all}\:{n}\:{we}\:{deduce} \\ $$$${that}\:\left({u}_{{n}} {v}_{{n}} \right)\:{is}\:{constant} \\ $$
