
Question Number 167158 by mnjuly1970 last updated on 08/Mar/22
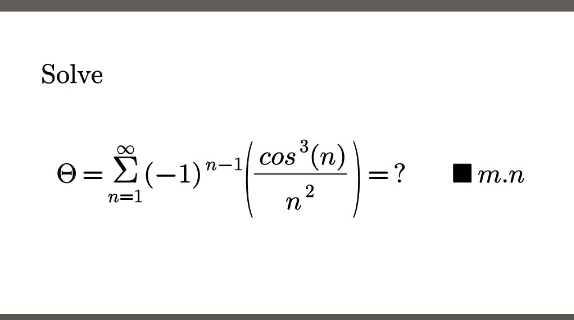
Answered by mindispower last updated on 10/Mar/22

$${cos}\left(\mathrm{3}{n}\right)=\mathrm{4}{cos}^{\mathrm{3}} \left({n}\right)−\mathrm{3}{cos}\left({n}\right)\Rightarrow{cos}^{\mathrm{3}} \left({n}\right)=\frac{{cos}\left(\mathrm{3}{n}\right)+\mathrm{3}{cos}\left({n}\right)}{\mathrm{4}} \\ $$$$\Theta=\frac{\mathrm{1}}{\mathrm{4}}{Re}\left\{\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}^{\mathrm{2}} }.\left({e}^{\mathrm{3}{in}} +\mathrm{3}{e}^{{in}} \right)\right\} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{Re}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{e}^{\mathrm{3}{i}} \right)^{{n}} }{{n}^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{4}}{Re}\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−{e}^{{i}} \right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}\left({Re}\left({Li}_{\mathrm{2}} \left(−{e}^{\mathrm{3}{i}} \right)+\mathrm{3}{Li}_{\mathrm{2}} \left(−{e}^{{i}} \right)\right)\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\left({Li}_{\mathrm{2}} \left(−{e}^{\mathrm{3}{i}} \right)+{Li}_{\mathrm{2}} \left(−{e}^{−\mathrm{3}{i}} \right)+\mathrm{3}{Li}_{\mathrm{2}} \left(−{e}^{{i}} \right)+\mathrm{3}{Li}_{\mathrm{2}} \left(−{e}^{−{i}} \right)\right) \\ $$$${li}_{\mathrm{2}} \left({a}\right)+{li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}}\right)=−\zeta\left(\mathrm{2}\right)−\frac{{ln}^{\mathrm{2}} \left(−{a}\right)}{\mathrm{2}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}\left(−\zeta\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({e}^{\mathrm{3}{i}} \right)+\mathrm{3}\left(−\zeta\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left({e}^{{i}} \right)\right)\right. \\ $$$$=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{6}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\frac{\mathrm{6}}{\mathrm{8}}\: \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 12/Mar/22

$$\:\:\:\:\:\:\:{very}\:{nice}\:{solution}\:\:{sir} \\ $$$$\:\:\:\:\:\:\:\:{grateful}\:{sir}\:{power} \\ $$
