
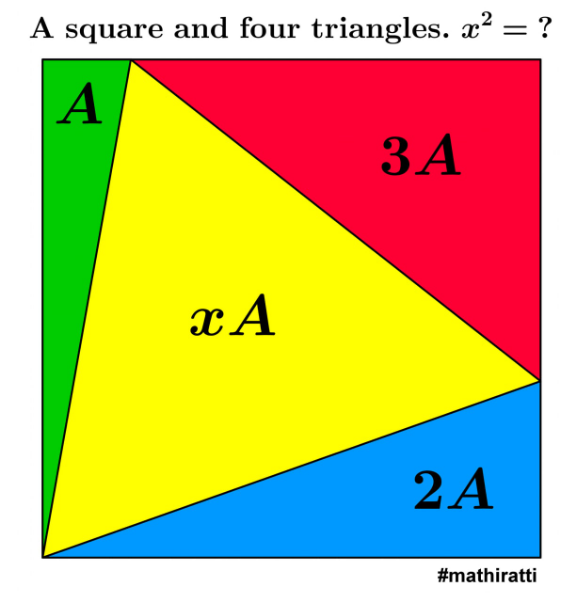
Question Number 167152 by cortano1 last updated on 08/Mar/22
Commented by som(math1967) last updated on 08/Mar/22

$$\:{x}^{\mathrm{2}} =\mathrm{28}\:? \\ $$
Commented by cortano1 last updated on 08/Mar/22

$$\mathrm{yes} \\ $$
Answered by som(math1967) last updated on 08/Mar/22
Commented by som(math1967) last updated on 08/Mar/22
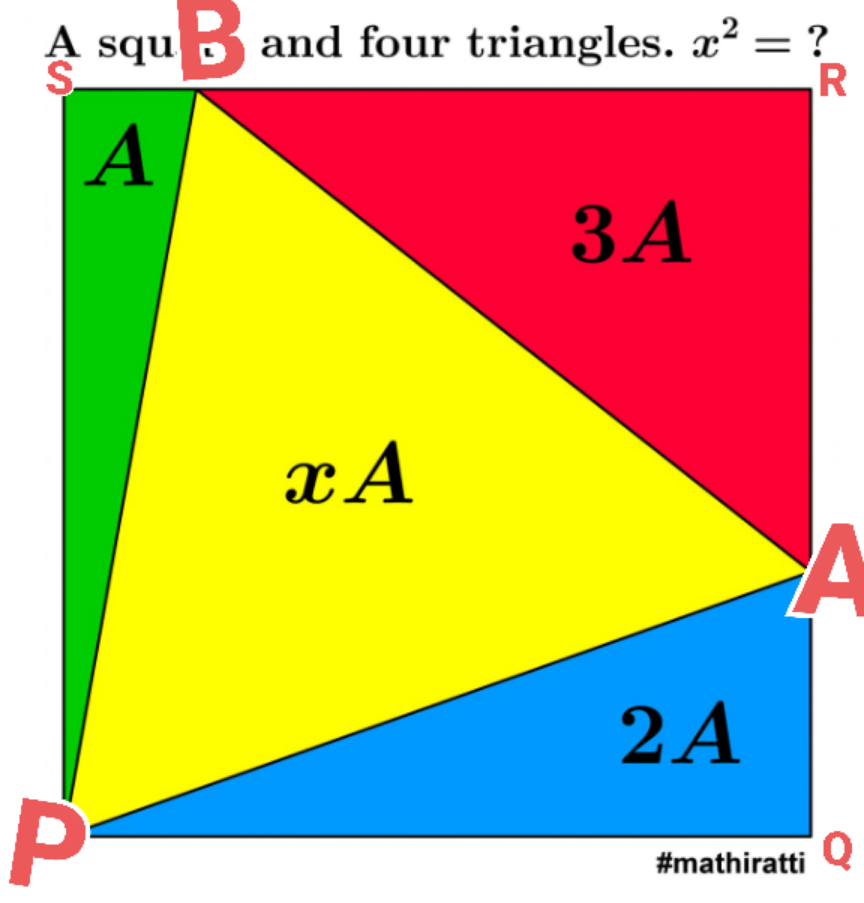
![let SB=l side of square=a A=((al)/2) 2A=((a×AQ)/2) ∴a×AQ=2al⇒AQ=2l ∴BR=a−l AR=a−2l 3A=(((a−l)(a−2l))/2) ((3al)/2)=((a^2 −3al+2l^2 )/2) ⇒a^2 −6al+2l^2 =0 ⇒(a^2 /l^2 ) −((6a)/l) +2=0 ∴ (a/l)=((6+(√(28)))/2)=3+(√7) [ ∵(a/l)>1 ∴ −ve rejected] A=((al)/2)=(a^2 /(2(3+(√7)))) ar. of yellow △=Y(let) Y=a^2 −6A =a^2 −((3a^2 )/((3+(√7))))=(((√7)a^2 )/((3+(√7)))) (Y/A)=2(√7)⇒Y=2(√7)A ∴x=2(√7) ⇒x^2 =28](Q167156.png)
$${let}\:{SB}={l}\:{side}\:{of}\:{square}={a} \\ $$$${A}=\frac{{al}}{\mathrm{2}}\:\: \\ $$$$\mathrm{2}{A}=\frac{{a}×{AQ}}{\mathrm{2}} \\ $$$$\therefore{a}×{AQ}=\mathrm{2}{al}\Rightarrow{AQ}=\mathrm{2}{l} \\ $$$$\therefore{BR}={a}−{l}\:\:\:{AR}={a}−\mathrm{2}{l} \\ $$$$\:\mathrm{3}{A}=\frac{\left({a}−{l}\right)\left({a}−\mathrm{2}{l}\right)}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}{al}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} −\mathrm{3}{al}+\mathrm{2}{l}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\:\Rightarrow{a}^{\mathrm{2}} −\mathrm{6}{al}+\mathrm{2}{l}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\frac{{a}^{\mathrm{2}} }{{l}^{\mathrm{2}} }\:−\frac{\mathrm{6}{a}}{{l}}\:+\mathrm{2}=\mathrm{0} \\ $$$$\therefore\:\frac{{a}}{{l}}=\frac{\mathrm{6}+\sqrt{\mathrm{28}}}{\mathrm{2}}=\mathrm{3}+\sqrt{\mathrm{7}}\:\left[\:\because\frac{{a}}{{l}}>\mathrm{1}\:\therefore\:−{ve}\:{rejected}\right] \\ $$$${A}=\frac{{al}}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}\left(\mathrm{3}+\sqrt{\mathrm{7}}\right)} \\ $$$${ar}.\:{of}\:{yellow}\:\bigtriangleup={Y}\left({let}\right) \\ $$$${Y}={a}^{\mathrm{2}} −\mathrm{6}{A} \\ $$$$={a}^{\mathrm{2}} −\frac{\mathrm{3}{a}^{\mathrm{2}} }{\left(\mathrm{3}+\sqrt{\mathrm{7}}\right)}=\frac{\sqrt{\mathrm{7}}{a}^{\mathrm{2}} }{\left(\mathrm{3}+\sqrt{\mathrm{7}}\right)} \\ $$$$\:\:\frac{{Y}}{{A}}=\mathrm{2}\sqrt{\mathrm{7}}\Rightarrow{Y}=\mathrm{2}\sqrt{\mathrm{7}}{A} \\ $$$$\therefore{x}=\mathrm{2}\sqrt{\mathrm{7}}\:\Rightarrow{x}^{\mathrm{2}} =\mathrm{28} \\ $$
Commented by Tawa11 last updated on 10/Mar/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
