
Question Number 167066 by mathlove last updated on 05/Mar/22
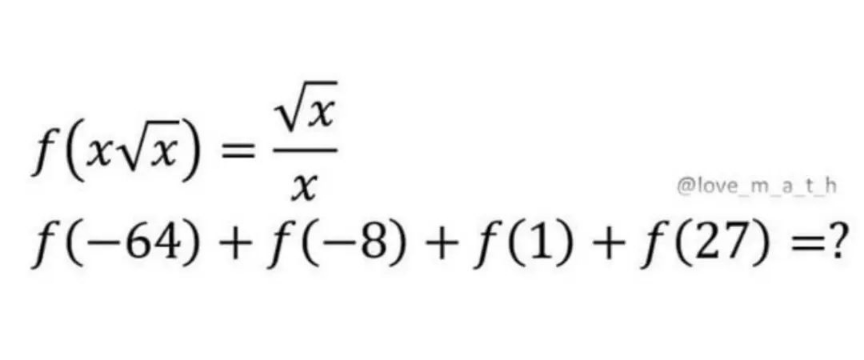
Commented by cortano1 last updated on 05/Mar/22
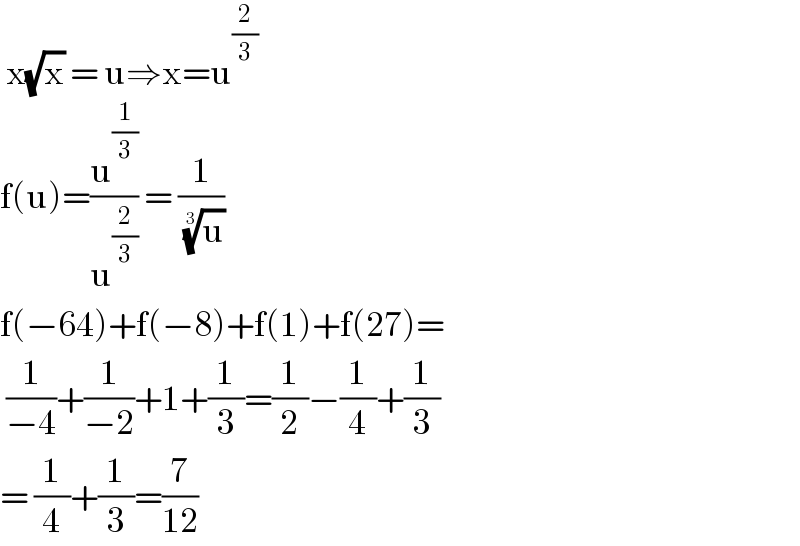
$$\:\mathrm{x}\sqrt{\mathrm{x}}\:=\:\mathrm{u}\Rightarrow\mathrm{x}=\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\mathrm{f}\left(\mathrm{u}\right)=\frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:=\:\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{u}}} \\ $$$$\mathrm{f}\left(−\mathrm{64}\right)+\mathrm{f}\left(−\mathrm{8}\right)+\mathrm{f}\left(\mathrm{1}\right)+\mathrm{f}\left(\mathrm{27}\right)= \\ $$$$\:\frac{\mathrm{1}}{−\mathrm{4}}+\frac{\mathrm{1}}{−\mathrm{2}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{7}}{\mathrm{12}} \\ $$
