
Question Number 166592 by Ari last updated on 22/Feb/22
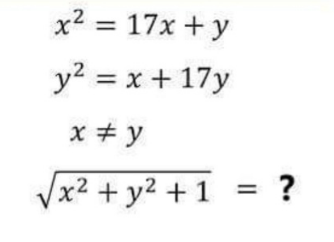
Answered by nurtani last updated on 23/Feb/22
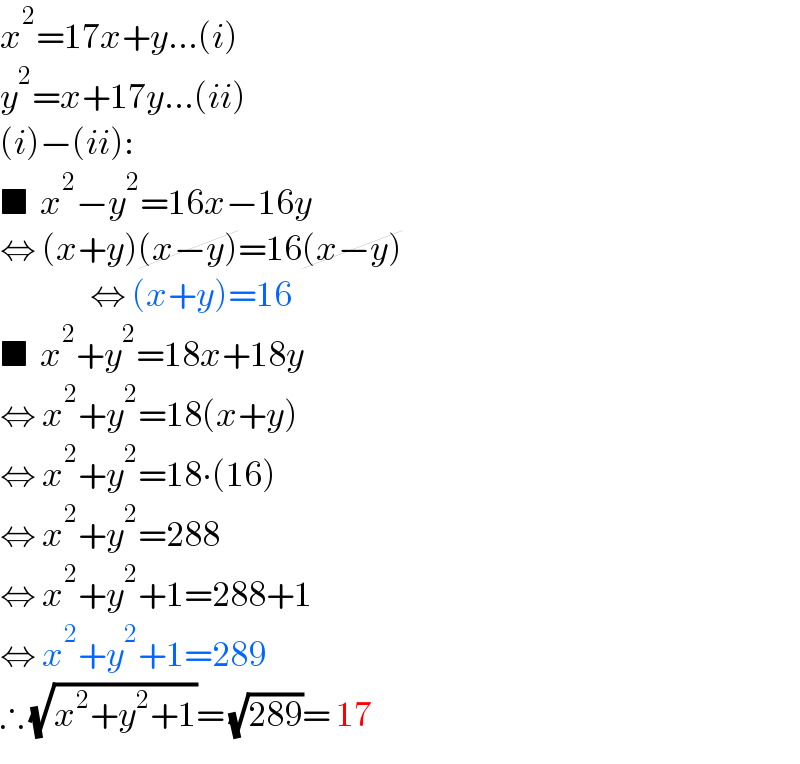
$${x}^{\mathrm{2}} =\mathrm{17}{x}+{y}...\left({i}\right) \\ $$$${y}^{\mathrm{2}} ={x}+\mathrm{17}{y}...\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$$\blacksquare\:\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{16}{x}−\mathrm{16}{y} \\ $$$$\Leftrightarrow\:\left({x}+{y}\right)\cancel{\left({x}−{y}\right)}=\mathrm{16}\cancel{\left({x}−{y}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Leftrightarrow\:\left({x}+{y}\right)=\mathrm{16} \\ $$$$\blacksquare\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{18}{x}+\mathrm{18}{y} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{18}\left({x}+{y}\right) \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{18}\centerdot\left(\mathrm{16}\right) \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{288} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{288}+\mathrm{1} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}=\mathrm{289} \\ $$$$\therefore\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{1}}=\:\sqrt{\mathrm{289}}=\:\mathrm{17}\: \\ $$
Commented by Ari last updated on 23/Feb/22
and -17
