
Question Number 166580 by mkam last updated on 22/Feb/22
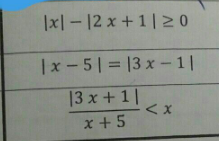
Answered by mahdipoor last updated on 22/Feb/22
![1) ⇒∣x∣≥∣2x+1∣⇒x^2 ≥4x^2 +4x+1⇒ 0≥3x^2 +4x+1=(3x+1)(x+1)⇒ x∈[−1,−1/3] 2) x−5=±(3x−1)⇒x=−2,3/2 3) i) x<−5 ⇒ x+5<0 , 3x+1<0 ⇒ −(3x+1)>(x+5)x⇒0>x^2 +8x+1⇒ x∈(−4−(√(15)),−4+(√(15))) ⇒x∈(−4−(√(15)),−5) ii)−1/3≥x>−5 ⇒ x+5>0 , 3x+1<0 ⇒ −(3x+1)<x(x+5)⇒0<x^2 +8x+1 ⇒ x∈]−4−(√(15)),−4+(√(15))[ ⇒x∈∅ iii)x≥−1/3 ⇒x+5>0 , 3x+1>0 ⇒ (3x+1)<x(x+5)⇒0<x^2 +2x−1⇒ x∈(−1−(√2),−1+(√2)) ⇒x∈[−1/3,−1+(√2)) ⇒iii∪ii∪i⇒ x∈(−4−(√(15)),−5)∪[−1/3,−1+(√2))](Q166582.png)
$$\left.\mathrm{1}\right) \\ $$$$\Rightarrow\mid{x}\mid\geqslant\mid\mathrm{2}{x}+\mathrm{1}\mid\Rightarrow{x}^{\mathrm{2}} \geqslant\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}\Rightarrow \\ $$$$\mathrm{0}\geqslant\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{1}=\left(\mathrm{3}{x}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)\Rightarrow \\ $$$${x}\in\left[−\mathrm{1},−\mathrm{1}/\mathrm{3}\right] \\ $$$$\left.\mathrm{2}\right) \\ $$$${x}−\mathrm{5}=\pm\left(\mathrm{3}{x}−\mathrm{1}\right)\Rightarrow{x}=−\mathrm{2},\mathrm{3}/\mathrm{2} \\ $$$$\left.\mathrm{3}\right) \\ $$$$\left.{i}\right)\:{x}<−\mathrm{5}\:\Rightarrow\:{x}+\mathrm{5}<\mathrm{0}\:,\:\mathrm{3}{x}+\mathrm{1}<\mathrm{0}\:\Rightarrow \\ $$$$−\left(\mathrm{3}{x}+\mathrm{1}\right)>\left({x}+\mathrm{5}\right){x}\Rightarrow\mathrm{0}>{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{1}\Rightarrow \\ $$$${x}\in\left(−\mathrm{4}−\sqrt{\mathrm{15}},−\mathrm{4}+\sqrt{\mathrm{15}}\right) \\ $$$$\Rightarrow{x}\in\left(−\mathrm{4}−\sqrt{\mathrm{15}},−\mathrm{5}\right) \\ $$$$\left.{ii}\right)−\mathrm{1}/\mathrm{3}\geqslant{x}>−\mathrm{5}\:\Rightarrow\:{x}+\mathrm{5}>\mathrm{0}\:,\:\mathrm{3}{x}+\mathrm{1}<\mathrm{0}\:\Rightarrow \\ $$$$−\left(\mathrm{3}{x}+\mathrm{1}\right)<{x}\left({x}+\mathrm{5}\right)\Rightarrow\mathrm{0}<{x}^{\mathrm{2}} +\mathrm{8}{x}+\mathrm{1}\:\Rightarrow \\ $$$$\left.{x}\in\right]−\mathrm{4}−\sqrt{\mathrm{15}},−\mathrm{4}+\sqrt{\mathrm{15}}\left[\right. \\ $$$$\Rightarrow{x}\in\varnothing \\ $$$$\left.{iii}\right){x}\geqslant−\mathrm{1}/\mathrm{3}\:\Rightarrow{x}+\mathrm{5}>\mathrm{0}\:,\:\mathrm{3}{x}+\mathrm{1}>\mathrm{0}\:\Rightarrow \\ $$$$\left(\mathrm{3}{x}+\mathrm{1}\right)<{x}\left({x}+\mathrm{5}\right)\Rightarrow\mathrm{0}<{x}^{\mathrm{2}} +\mathrm{2}{x}−\mathrm{1}\Rightarrow \\ $$$${x}\in\left(−\mathrm{1}−\sqrt{\mathrm{2}},−\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}\in\left[−\mathrm{1}/\mathrm{3},−\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{iii}\cup{ii}\cup{i}\Rightarrow \\ $$$${x}\in\left(−\mathrm{4}−\sqrt{\mathrm{15}},−\mathrm{5}\right)\cup\left[−\mathrm{1}/\mathrm{3},−\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
