Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 166392 by leicianocosta last updated on 19/Feb/22

Answered by som(math1967) last updated on 19/Feb/22

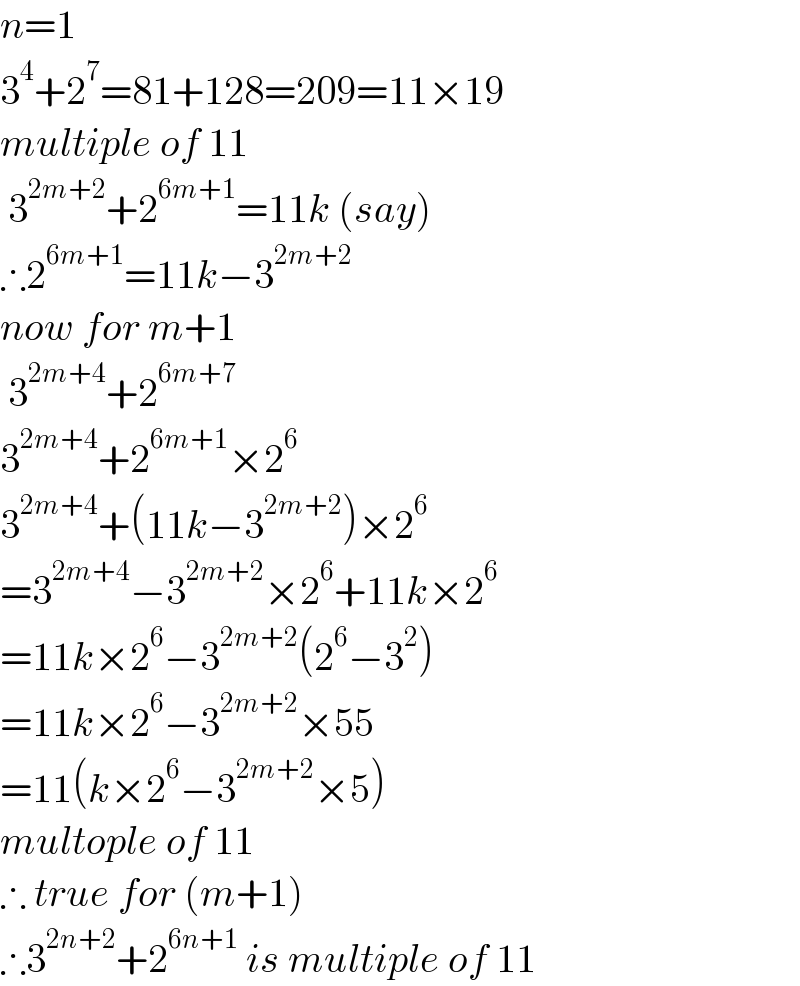
n=1 3^4 +2^7 =81+128=209=11×19 multiple of 11 3^(2m+2) +2^(6m+1) =11k (say) ∴2^(6m+1) =11k−3^(2m+2) now for m+1 3^(2m+4) +2^(6m+7) 3^(2m+4) +2^(6m+1) ×2^6 3^(2m+4) +(11k−3^(2m+2) )×2^6 =3^(2m+4) −3^(2m+2) ×2^6 +11k×2^6 =11k×2^6 −3^(2m+2) (2^6 −3^2 ) =11k×2^6 −3^(2m+2) ×55 =11(k×2^6 −3^(2m+2) ×5) multople of 11 ∴ true for (m+1) ∴3^(2n+2) +2^(6n+1) is multiple of 11

$${n}=\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{4}} +\mathrm{2}^{\mathrm{7}} =\mathrm{81}+\mathrm{128}=\mathrm{209}=\mathrm{11}×\mathrm{19} \\ $$$${multiple}\:{of}\:\mathrm{11} \\ $$$$\:\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} +\mathrm{2}^{\mathrm{6}{m}+\mathrm{1}} =\mathrm{11}{k}\:\left({say}\right) \\ $$$$\therefore\mathrm{2}^{\mathrm{6}{m}+\mathrm{1}} =\mathrm{11}{k}−\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} \\ $$$${now}\:{for}\:{m}+\mathrm{1} \\ $$$$\:\mathrm{3}^{\mathrm{2}{m}+\mathrm{4}} +\mathrm{2}^{\mathrm{6}{m}+\mathrm{7}} \\ $$$$\mathrm{3}^{\mathrm{2}{m}+\mathrm{4}} +\mathrm{2}^{\mathrm{6}{m}+\mathrm{1}} ×\mathrm{2}^{\mathrm{6}} \\ $$$$\mathrm{3}^{\mathrm{2}{m}+\mathrm{4}} +\left(\mathrm{11}{k}−\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} \right)×\mathrm{2}^{\mathrm{6}} \\ $$$$=\mathrm{3}^{\mathrm{2}{m}+\mathrm{4}} −\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} ×\mathrm{2}^{\mathrm{6}} +\mathrm{11}{k}×\mathrm{2}^{\mathrm{6}} \\ $$$$=\mathrm{11}{k}×\mathrm{2}^{\mathrm{6}} −\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} \left(\mathrm{2}^{\mathrm{6}} −\mathrm{3}^{\mathrm{2}} \right) \\ $$$$=\mathrm{11}{k}×\mathrm{2}^{\mathrm{6}} −\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} ×\mathrm{55} \\ $$$$=\mathrm{11}\left({k}×\mathrm{2}^{\mathrm{6}} −\mathrm{3}^{\mathrm{2}{m}+\mathrm{2}} ×\mathrm{5}\right) \\ $$$${multople}\:{of}\:\mathrm{11} \\ $$$$\therefore\:{true}\:{for}\:\left({m}+\mathrm{1}\right) \\ $$$$\therefore\mathrm{3}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{2}^{\mathrm{6}{n}+\mathrm{1}} \:{is}\:{multiple}\:{of}\:\mathrm{11} \\ $$

Answered by JDamian last updated on 19/Feb/22

q=3^(2n+2) +2^(6n+1) =3^(2(n+1)) +2^(5n+n+1) q=9^(n+1) +2^(n+1) ∙32^n r=q mod 11 r=[(11−2)^(n+1) +2^(n+1) (33−1)^n ] mod 11= =[(−2)^(n+1) +2∙2^n ∙(−1)^n ] mod 11= =[(−2)(−2)^n +2∙(−2)^n ] mod 11= =[(−2+2)∙(−2)^n ] mod 11= =[0∙(−2)^n ] mod 11= =0

$${q}=\mathrm{3}^{\mathrm{2}{n}+\mathrm{2}} +\mathrm{2}^{\mathrm{6}{n}+\mathrm{1}} =\mathrm{3}^{\mathrm{2}\left({n}+\mathrm{1}\right)} +\mathrm{2}^{\mathrm{5}{n}+{n}+\mathrm{1}} \\ $$$${q}=\mathrm{9}^{{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{32}^{{n}} \\ $$$$ \\ $$$${r}={q}\:{mod}\:\mathrm{11} \\ $$$${r}=\left[\left(\mathrm{11}−\mathrm{2}\right)^{{n}+\mathrm{1}} +\mathrm{2}^{{n}+\mathrm{1}} \left(\mathrm{33}−\mathrm{1}\right)^{{n}} \right]\:{mod}\:\mathrm{11}= \\ $$$$=\left[\left(−\mathrm{2}\right)^{{n}+\mathrm{1}} +\mathrm{2}\centerdot\mathrm{2}^{{n}} \centerdot\left(−\mathrm{1}\right)^{{n}} \right]\:{mod}\:\mathrm{11}= \\ $$$$=\left[\left(−\mathrm{2}\right)\left(−\mathrm{2}\right)^{\boldsymbol{{n}}} +\mathrm{2}\centerdot\left(−\mathrm{2}\right)^{\boldsymbol{{n}}} \right]\:{mod}\:\mathrm{11}= \\ $$$$=\left[\left(−\mathrm{2}+\mathrm{2}\right)\centerdot\left(−\mathrm{2}\right)^{{n}} \right]\:{mod}\:\mathrm{11}= \\ $$$$=\left[\mathrm{0}\centerdot\left(−\mathrm{2}\right)^{{n}} \right]\:{mod}\:\mathrm{11}= \\ $$$$=\mathrm{0} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com